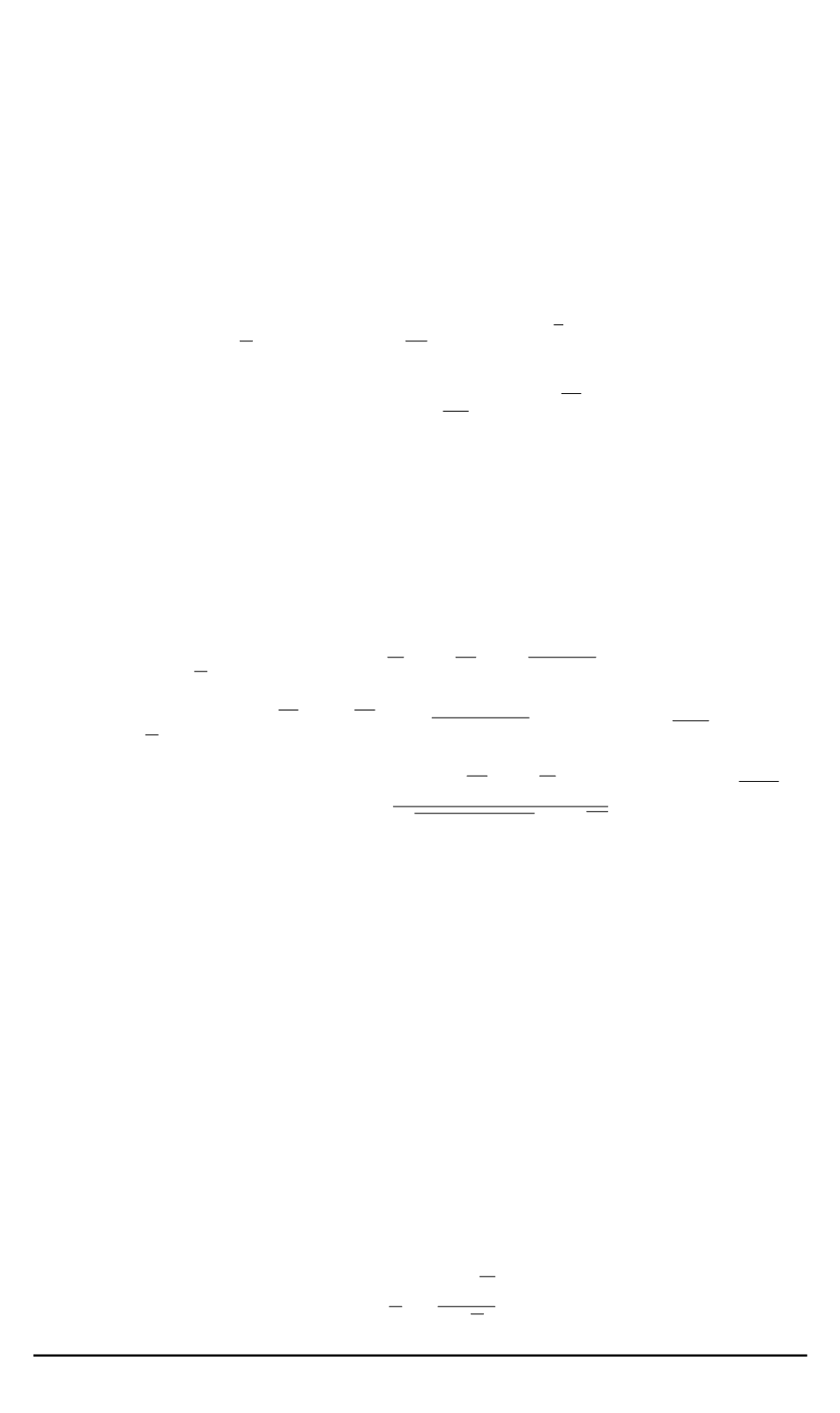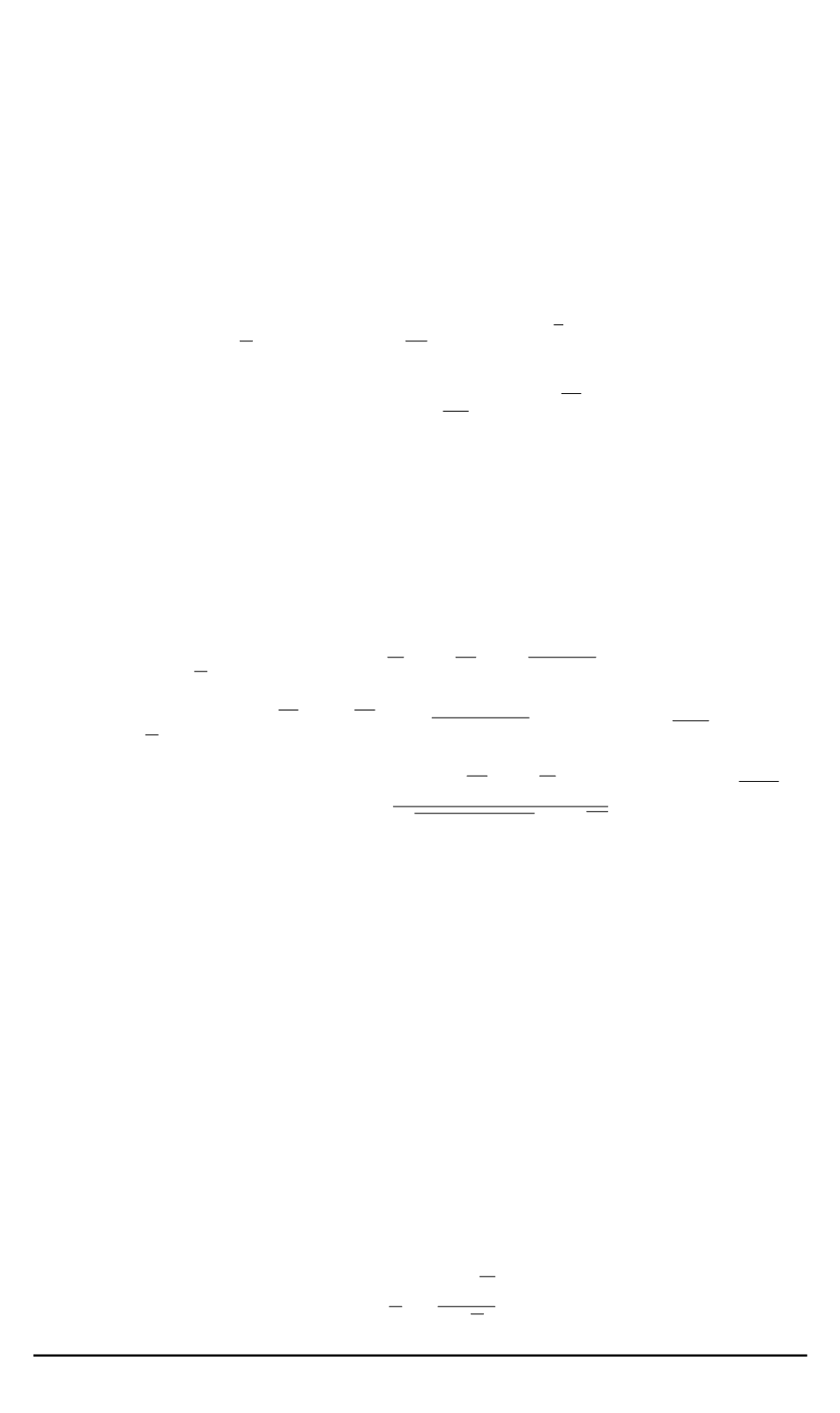
Z
(
t
) =
t
Z
0
[
δ
(
t
−
τ
)
−
R
(
t
−
τ
)] ˜
ξ
(
τ
)
dτ.
(21)
Используя метод описания немарковских случайных процессов, из-
ложенный в работе [7], для одномерной и
L
-мерной характеристиче-
ских функций случайного процесса
Z
(
t
)
, задаваемого интегральным
уравнением (21), для не слишком больших
t
(
t
≤
10
c) и
A
1
с
−
1
получим
g
1
(
λ
;
t
) = exp
−
1
2
˜
σλ
2
A
2
B
2
ln
t
δt
−
4
ABC
√
t
+
+
C
2
−
8
A
2
B
2
t
+
16
3
A
2
BC
√
t
3
+ 8
A
4
B
2
t
2
,
(22)
g
L
(
λ
1
, . . . , λ
L
;
t
1
, . . . , t
L
) = exp
"
−
˜
σ
L
X
l
=1
L
X
k
=1
λ
l
λ
k
Q
lk
(
t
l
, t
k
)
#
.
(23)
Здесь
˜
σ
— интенсивность случайного процесса
˜
ξ
(
t
)
,
δt
— малая поло-
жительная величина, а функция
Q
lk
(
t
l
, t
k
)
имеет вид
Q
lk
(
t
l
, t
k
) =
1
2
C
2
t
k
−
ABC
√
t
l
+
√
t
k
− √
t
l
−
t
k
+
+
4
3
A
2
BC
q
t
3
l
+
q
t
3
k
−
p
(
t
l
−
t
k
)
3
−
4
A
3
B
2
√
t
k
t
l
+
+
A
2
B
2
1 + 8
A
2
(
t
l
−
t
k
) ln
√
t
k
+
√
t
l
√
t
l
−
t
k
+
δt
+
√
δt
+ 4
A
4
B
2
q
t
k
t
3
l
.
(24)
В выражениях (22) и (24)
C
=
−
A
+
πA
2
B
2
. График функции
g
1
(
λ
;
t
)
при различных
t
,
˜
σ
= 1
м
2
/с
3
,
А
= 0
,
01
с
−
1
,
В
= 0
,
1
с
1
/
2
показан на
рис. 4.
Многомерные характеристические функции
g
L
(
λ
1
, . . . , λ
L
;
t
1
, . . . , t
L
)
,
задаваемые выражением (23), позволяют найти моменты любого по-
рядка случайного процесса
Z
(
t
)
[6]. В частности, для корреляционной
функции получим
h
Z
(
t
1
)
Z
(
t
2
)
i
= 2˜
σQ
12
(
t
1
, t
2
)
.
(25)
Для нахождения спектральной плотности случайного процесса
Z
(
t
)
найдем преобразование Лапласа уравнения (12) при
˜
F
0
(
t
) = 0
,
что позволяет записать его в изображениях:
ˆ
Z
(
p
) 1 +
A
1
p
+
B
√
π
√
p
= ˆ
ξ
(
p
)
(26)
8
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4