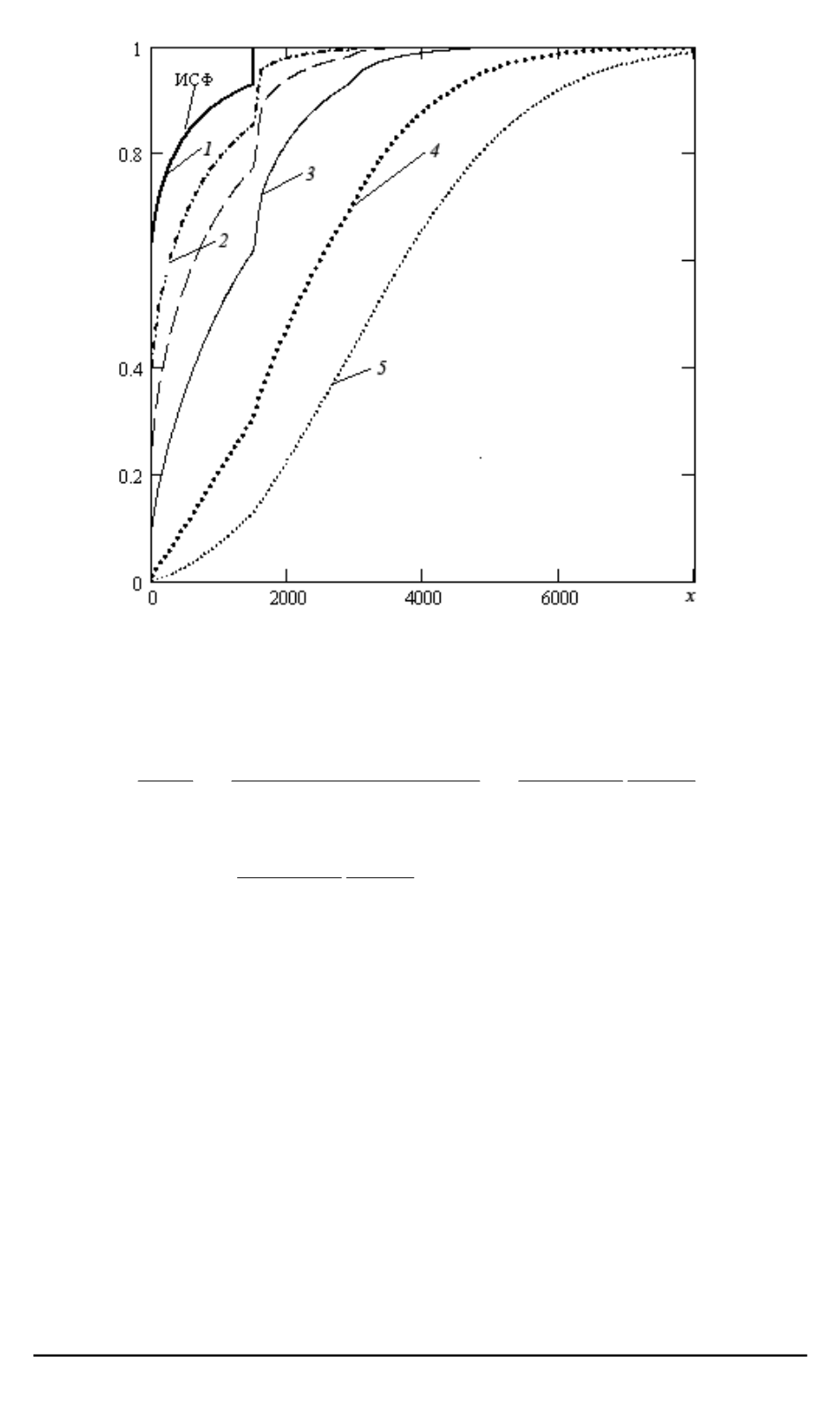
Рис. 3. Графики функций распределения:
ИСФ — исходная;
1
— 2-х,
2
— 3-х,
3
— 5-и,
4
— 10-ти,
5
— 15-и кратные свертки
Из выражений (37) и (40) получаем
B
k
n
B
k
−
1
n
=
C
k
n
a
k
н
(1
−
a
н
)
n
−
k
C
k
−
1
n
a
k
−
1
н
(1
−
a
н
)
n
−
k
+1
=
n
−
k
+ 1
k
a
н
1
−
a
н
,
(41)
откуда
B
k
n
=
n
−
k
+ 1
k
a
н
1
−
a
н
B
k
−
1
n
, k
= 1
,
2
, . . . , n.
(42)
B
0
n
найдем, используя формулу (37):
B
0
n
=
C
0
n
(1
−
a
н
)
n
= (1
−
a
н
)
n
.
(43)
Формулы (42) и (43) позволяют рассчитать все коэффициенты
B
k
n
,
k
= 0
,
1
,
2
, . . . , n
.
Естественное ограничение на расчет по выведенным формулам
возникает в случае, когда значение
B
k
n
окажется больше предельного
числа
10
307
. Этому числу соответствует предельная кратность сверт-
ки
n
= 420
. При необходимости исчисления сверток более высокой
кратности можно вновь воспользоваться предельными теоремами, не
обращая внимания на разрывность свертываемых распределений.
На рис. 3 и 4 приведены примеры расчета сверток с использова-
нием предложенной методики. Из рисунков видно, что если свертки
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3
117


