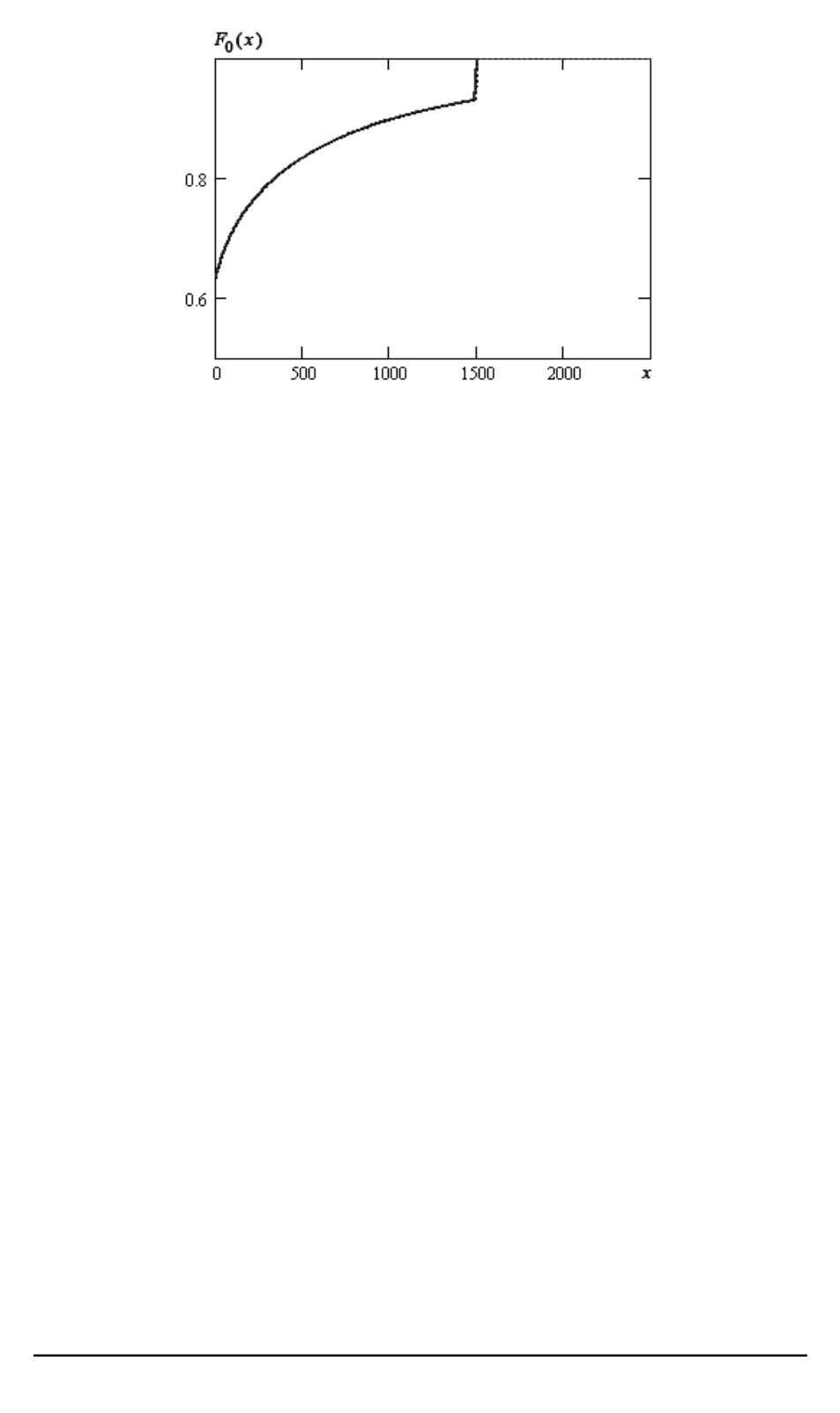
Рис. 1. Функция распределения страхового ущерба от единичного страхового
случая с учетом франшизы и лимита
Функция распределения случайной величины
Y
может быть фор-
мально вычислена с помощью рекуррентной процедуры вида
F
(1)
(
x
) =
F
0
(
x
)
,
F
(
k
)
(
x
) =
x
Z
0
F
(
k
−
1)(
x
−
y
)
dF
0
(
y
)
, k
= 2
,
3
, . . . n.
.
(5)
При
k
=
n
соответствующая свертка дает искомую функцию рас-
пределения
ˉ
F
(
x
)
случайной величины
Y
:
ˉ
F
(
x
) =
P
{
Y < x
}
=
F
(
n
)
(
x
)
,
(6)
где
F
(
n
)
(
x
)
—
n
-кратная свертка функции распределения (4).
При невысокой кратности свертки
n
такая процедура, будучи ре-
ализована численно, дает вполне удовлетворительный результат. Од-
нако если число слагаемых измеряется многими десятками и даже
сотнями единиц, то описанная процедура становится трудно реализу-
емой из-за чрезвычайной громоздкости вычислений. При разрывном
характере исходной функции
F
0
(
x
)
, обусловленном указанными вы-
ше причинами, добавляются трудности компьютерного моделирова-
ния разрывных функций распределения.
При решении рассмотренной задачи определения функции рас-
пределения суммы большого числа независимых случайных вели-
чин представляется вполне естественной попытка воспользоваться
предельной теоремой для суммы независимых случайных величин
[2, гл. 4, п. 4]. Однако, как показывают компьютерные эксперименты,
сходимость суммы независимых случайных величин к безгранично-
делимому закону распределения (например, нормальному или гамма-
распределению) при разрывном характере
F
0
(
x
)
настолько медленная,
108
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3


