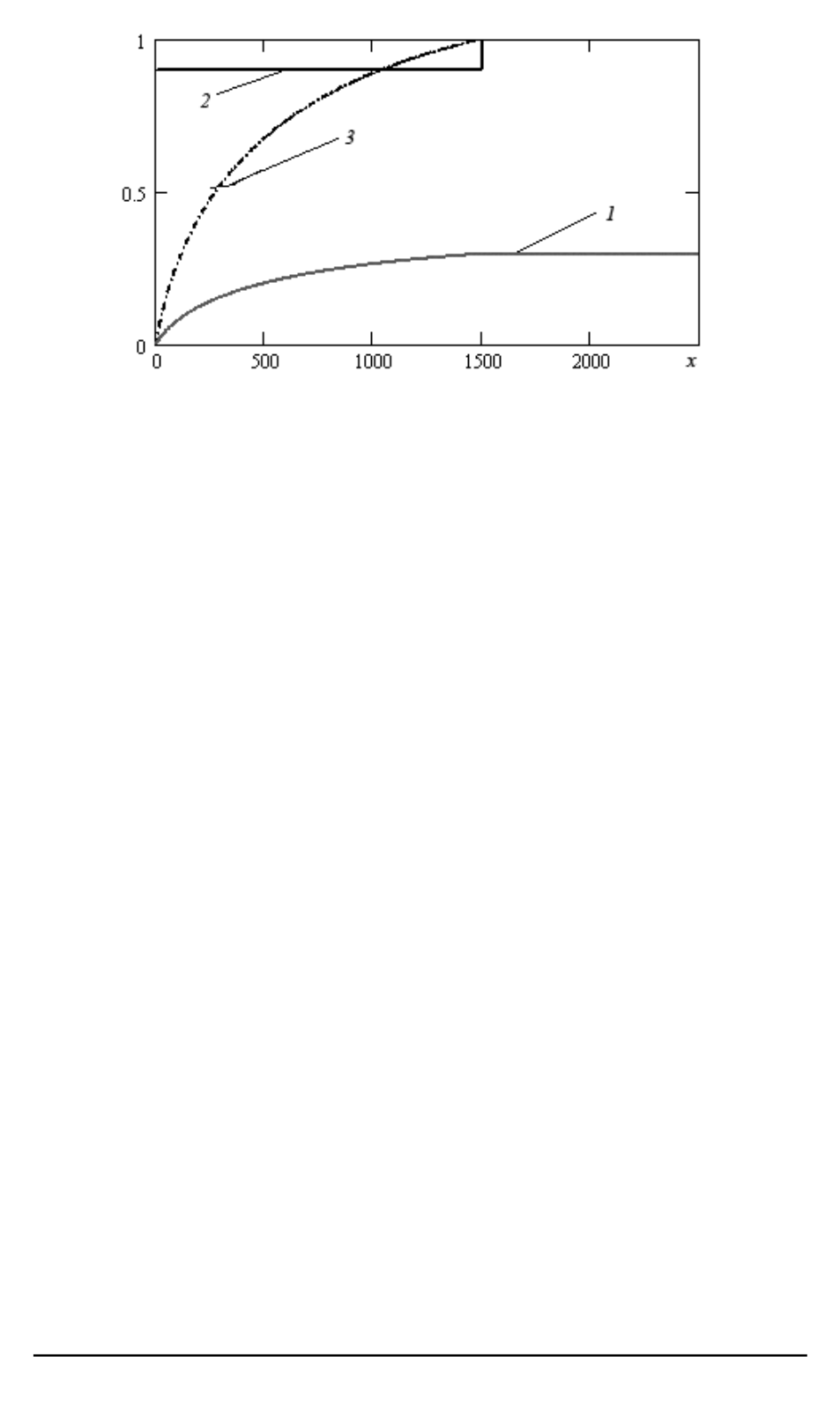
Рис. 2. Графики функций распределения:
1
— непрерывная;
2
— разрывная;
3
— нормированная к единице непрерывная функ-
ция
что воспользоваться предельными теоремами “в лоб” практически не
удается (см. рис. 3). Тем не менее, результатами работы [2] можно вос-
пользоваться и весьма эффективно, если удается исходную функцию
F
0
(
x
)
представить в виде суммы двух составляющих — непрерыв-
ной
F
н
(
x
)
и ступенчатой
F
с
(
x
)
(рис. 2). Именно предположение о воз-
можности представления свертываемой функции
F
0
(
x
)
в виде суммы
непрерывной и ступенчатой составляющих лежит в основе предлагае-
мого в данной работе алгоритма исчисления сверток
F
(
n
)
0
(
x
)
высокой
кратности.
Вывод расчетных соотношений.
Будем считать известным отно-
сительно функции распределения
F
0
(
x
)
, что в точках
x
ν
,
ν
= 1
,
2
, . . . , m
,
эта функция имеет разрывы величиной
с
ν
,
с
ν
>
0
, т.е.
c
ν
= lim
ε
→
0
[
F
0
(
x
0
+
ε
)
−
F
0
(
x
ν
−
ε
)]
, ν
= 1
,
2
, . . . , m,
(7)
а в остальных точках
x
2
(0
,
∞
)
F
0
(
x
)
непрерывна. (Реально число
разрывов
m
невелико, обычно
m
≤
2
. . .
3)
. На основании выраже-
ний (7) можно построить ступенчатую составляющую функции
F
0
(
x
)
,
определив ее формулой
F
c
(
x
) =
m
X
ν
=1
c
ν
h
(
x
−
x
ν
)
,
(8)
где
h
(
∙
)
— функция единичного скачка (2).
Непрерывную составляющую функции
F
0
(
x
)
определим как раз-
ность
F
н
(
x
) =
F
0
(
x
)
−
F
c
(
x
)
.
(9)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3
109


