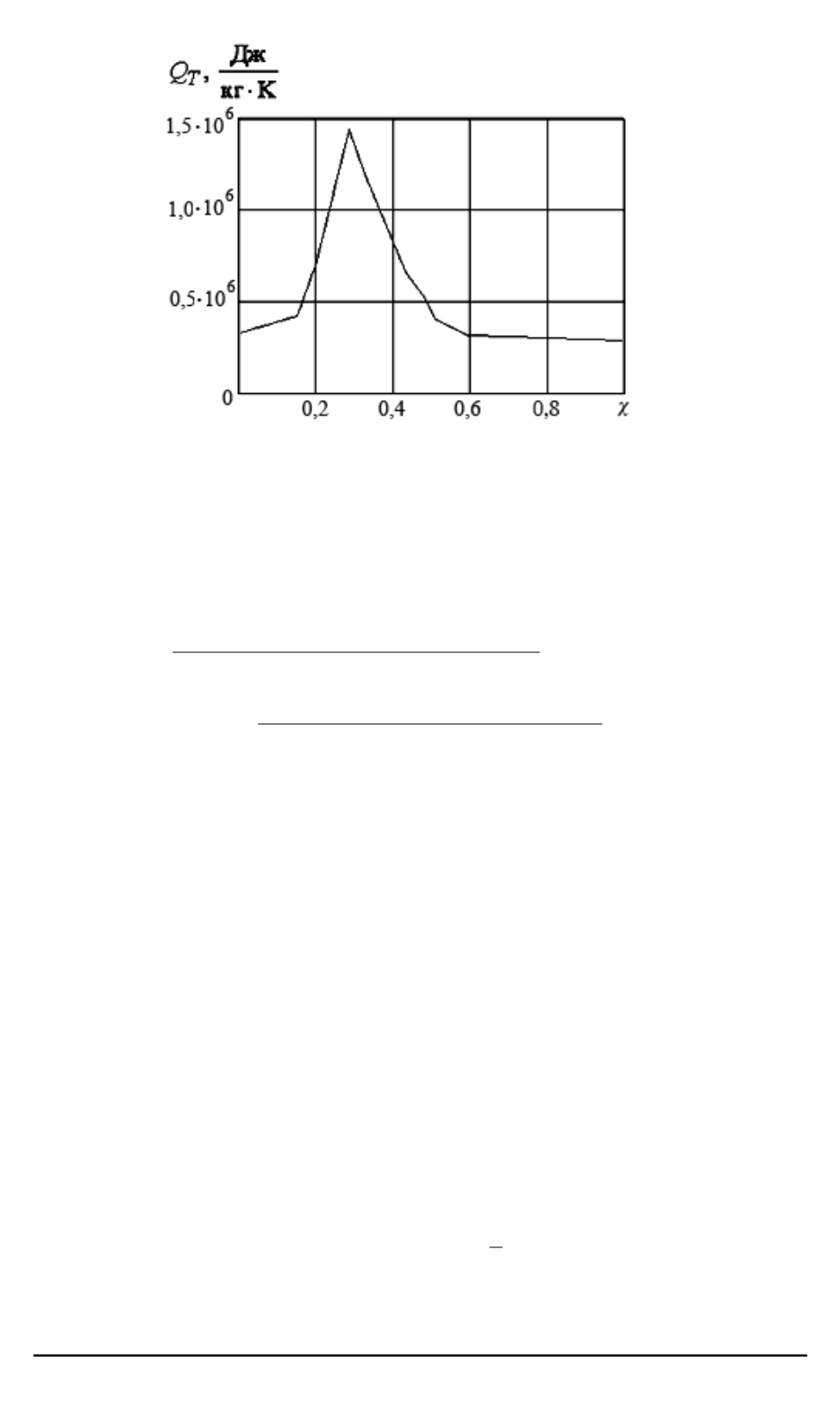
Рис. 1. Зависимость количества теплоты, переданного 1 кг материала никелида
титана при его нагреве на 1 K, от температуры
нагревании на 1К [ 3 ] (рис. 1), по соотношению (30) с использованием
неравенств (22) и равенства
c
σ
=
c
ε
+ 9
T
0
K α
(
T
) 2
:
ρc
down
ε
(
χ
)Δ
T
−
S
(Δ
T ,
Δ
χ , T , χ
)
ρ
Δ
χ
6
m
ε
(
χ
)
6
6
ρc
up
ε
(
χ
)Δ
T
−
S
(Δ
T ,
Δ
χ , T , χ
)
ρ
Δ
χ
,
(
31
)
m
down
ε
(
χ
)
θ/
(
T
0
χ
)
6
γ
ε
(
χ
)
6
m
up
ε
(
χ
)
θ/
(
T
0
χ
)
,
(
32
)
где
c
down
ε
, c
up
ε
— нижняя и верхняя границы удельной массовой те-
плоемкости материала (см. (22)),
m
down
ε
, m
up
ε
— нижняя и верхняя
границы удельной массовой конфигурационной теплоемкости мате-
риала,
S
(Δ
T,
Δ
χ, T, χ
)
— количество теплоты, переданное единице
объема материала для изменения температуры тела на
Δ
T
и измене-
ния доли мартенсита в материале на
Δ
χ
;
T, χ
— исходное значение
температуры и объемной доли мартенсита. Соотношения (31) и (32)
получены с учетом предположения, что диссипация энергии отсут-
ствует. Предположим, что объемная доля мартенсита линейно зависит
от температуры материала и
S
(Δ
T ,
Δ
χ , T , χ
)
будем вычислять как
площадь трапеции
S
(Δ
T ,
Δ
χ , T , χ
) =
1
2
(
Q
T
+Δ
T
) Δ
T.
Таким обра-
зом, в случае обратного фазового превращения, выражения (31), (32)
можно представить в следующем виде:
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 2
41


