Пусть
B
e
—
матрица
-
строка размера
1
×
N
e
с элементами
∂N
ei
/∂r
,
i
= 1
, N
e
.
Для отдельного КЭ получим
ρ
m
u
m
Z
V
e
c
p
N
e
т
N
e
dξ
d
{
T
e
}
dx
+
Z
V
e
λ
m
B
e
т
B
e
dξ
{
T
e
}
+
+
Z
S
1
e
αN
e
т
N
e
ds
{
T
e
}
=
Z
S
1
e
αT
г
N
e
т
ds.
(17)
Следует отметить
,
что слагаемые
,
содержащие поверхностные ин
-
тегралы
,
будут иметь ненулевые значения только для тех элементов
,
стороны которых будут принадлежать соответствующей поверхности
.
В матричной форме получим
[
c
e
]
d
{
T
}
dx
+ [
k
e
]
{
T
}
=
{
f
e
}
,
(18)
где
c
e
ln
=
c
p
ρu
m
Z
V
e
ϕ
l
ϕ
n
dξ,
k
e
ln
=
λ
m
Z
V
e
dϕ
l
dr
dϕ
n
dr
dξ
+
α
Z
S
1
e
ϕ
l
ϕ
n
ds, f
e
l
=
αT
г
Z
S
1
e
ϕ
l
ds.
Поскольку рассматриваемая задача решается в цилиндрической си
-
стеме координат
,
при интегрировании необходимо использовать якоби
-
ан преобразования координат
,
в данном случае равный
r
.
Эту функцию
также можно аппроксимировать в пределах КЭ выражением вида
r
≈
N
e
X
m
=1
r
e
m
ϕ
e
m
.
(19)
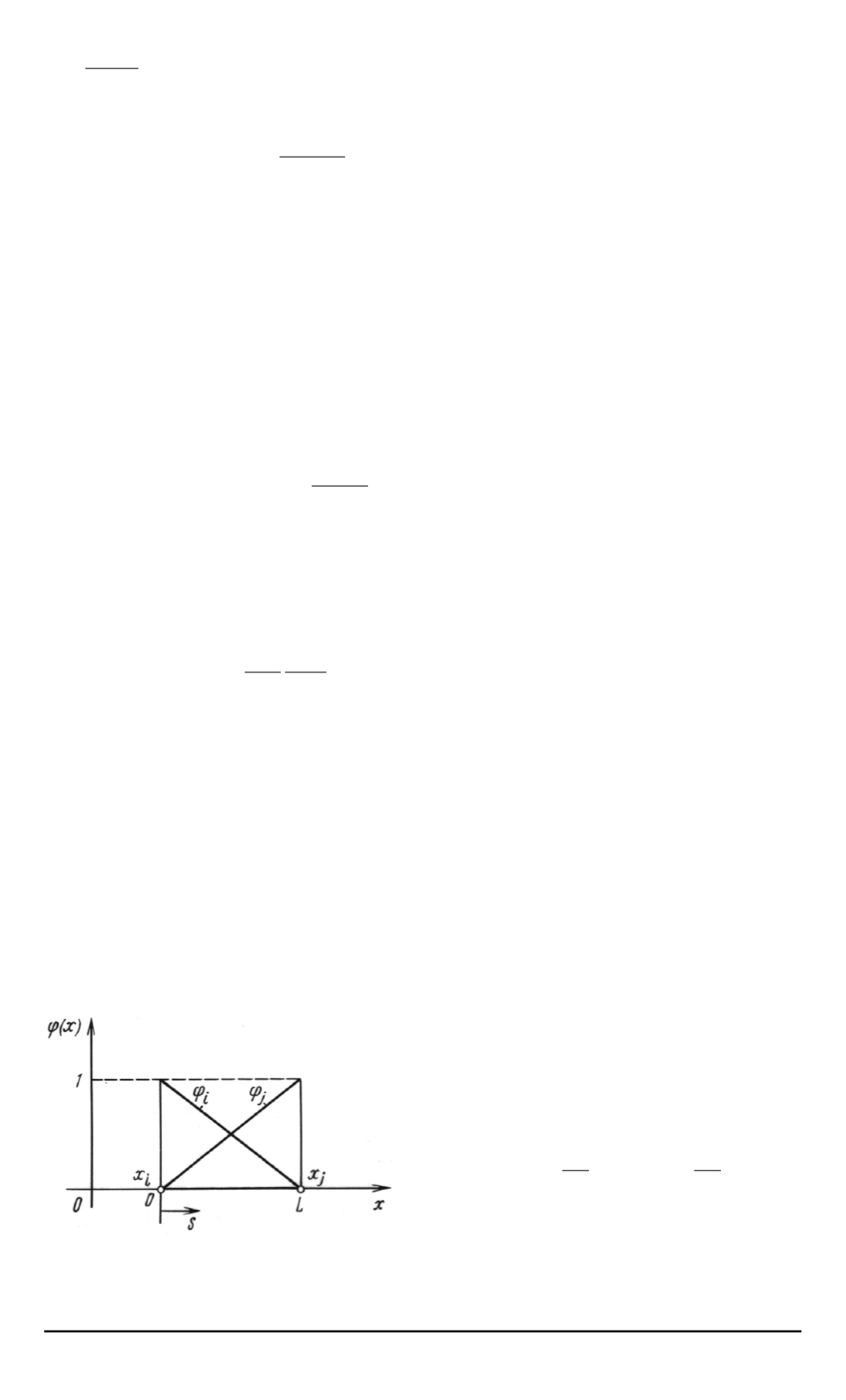
Рис
. 2.
Одномерный симплексный ко
-
нечный элемент
В качестве элемента разбие
-
ния подбирается одномерный сим
-
плексный КЭ
(
рис
. 2).
Функции формы для КЭ име
-
ют вид
N
e
1
= 1
−
s
e
L
e
, N
e
2
=
s
e
L
e
,
(20)
где
L
e
—
длина КЭ
;
s
e
—
локаль
-
ная координата
,
0
≤
s
e
≤
1
в преде
-
лах КЭ
.
84
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1


