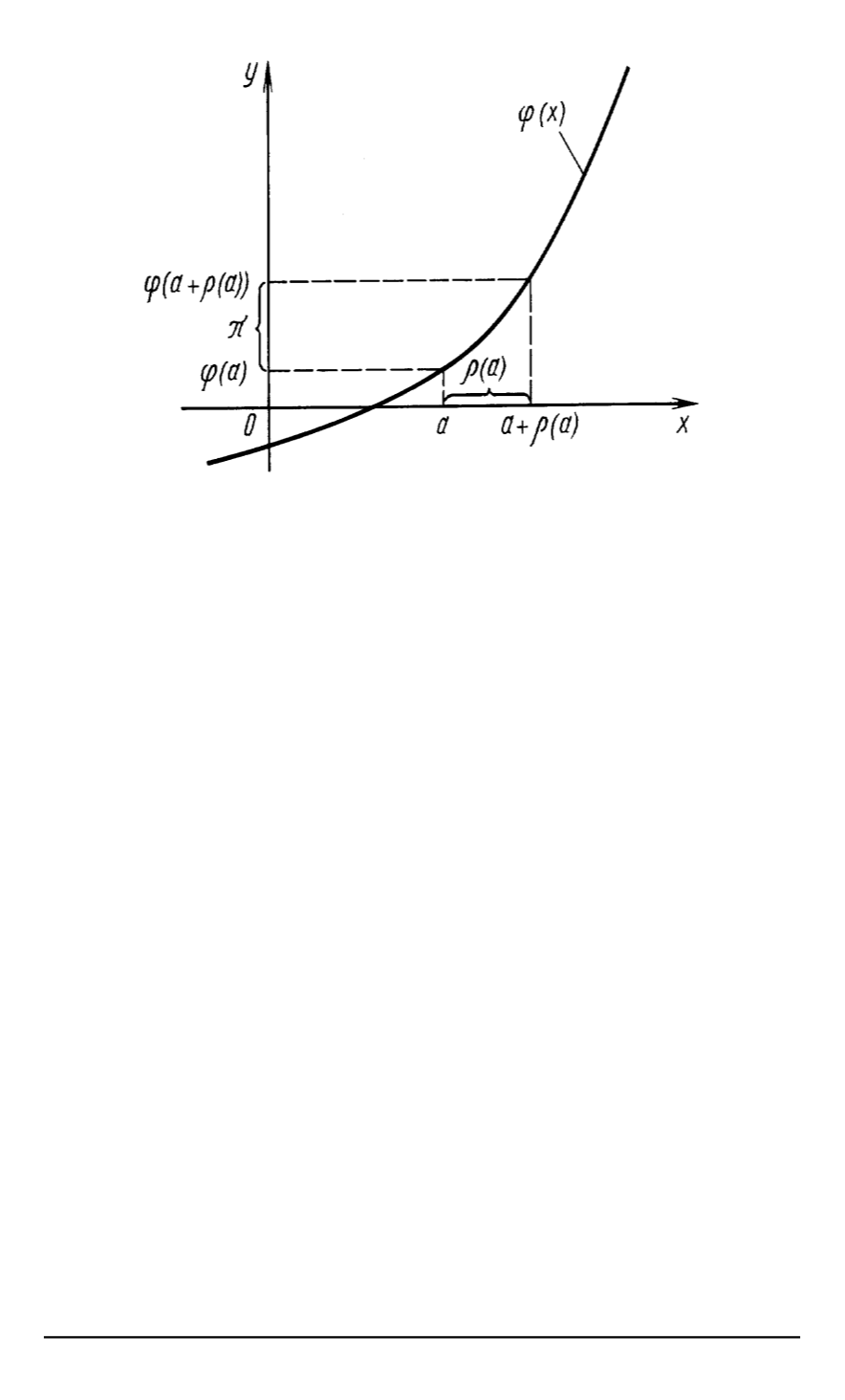
Рис
. 1.
К уравнению
(11)
Отсюда несложно определить
,
когда решение в следующий раз по
-
сле
x
=
a
обратится в нуль
.
Это произойдет в точке
x
=
b
,
в которой
ϕ
(
b
)
−
ϕ
(
a
) =
π.
Это соотношение определяет связь функций
ρ
(
x
)
и
ϕ
(
x
)
.
В самом деле
,
с учетом того
,
что сопряженной для
a
точкой является
,
по определению
ρ
(
x
)
,
точка
a
+
ρ
(
a
)
,
получим функциональную связь
(
рис
. 1)
ϕ
(
x
+
ρ
(
x
)) =
π
+
ϕ
(
x
)
.
(11)
Таким образом
,
функция смещения определяется через угловую ко
-
ординату
:
ρ
(
x
) =
ϕ
−
1
(
π
+
ϕ
(
x
))
−
x.
Можно сформулировать обратную задачу
.
Пусть задана функция
ρ
(
x
)
.
Требуется подобрать такую функцию плотности
p
(
x
)
,
чтобы за
-
данная
ρ
(
x
)
была функцией смещения для этой струны
.
В частном
случае
,
когда
ρ
(
x
)
≡
c
,
эта задача может быть решена
,
что и будет
сделано далее
.
Определение производной угловой функции для случая посто
-
янной функции смещения
.
Рассмотрим простейшую функцию сме
-
щения
ρ
(
x
)
≡
c
.
Уравнение
(11)
принимает вид
ϕ
(
x
+
c
) =
π
+
ϕ
(
x
)
.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2
15


