В промежутках между точками излома
{
x
k
}
уравнение
(13)
может
рассматриваться как классическое
:
y
00
= 0
.
Таким образом
,
функция
y
(
x
)
линейна
(
многочлен степени не бо
-
лее единицы
).
В точках
{
x
k
}
уравнение
(13)
преобразуется в условие
“
стыка
”
первой производной
:
(
y
0
(
x
k
+ 0)
−
y
0
(
x
k
−
0)) +
m
k
y
(
x
k
) = 0
.
Итак
,
любое решение
(
в терминах обобщенных функций
)
уравне
-
ния
(13)
задается формулами
y
(
x
) =
a
k
x
+
b
k
при
x
∈
[
x
k
−
1
;
x
k
]
,
(14)
где числа
a
k
,
b
k
удовлетворяют следующим условиям
:
a
k
x
k
+
b
k
=
a
k
+1
x
k
+
b
k
+1
(
условию непрерывности
)
и
a
k
+1
−
a
k
+
m
k
(
a
k
x
k
+
b
k
) = 0
(
условию
“
стыка
”).
Далее
,
следуя стратегии
,
описанной для струны
,
введем функцию
ω
(
x
)
.
Для случая
p
(
x
)
≡
0
она будет иметь вид
(10),
а для
p
(
x
)
,
соот
-
ветствующих выражению
(12),
вид
ω
(
x
) =
ω
k
(
x
) =
A
k
(
x
+
B
k
)
2
+
1
A
k
, A
k
>
0
при
x
∈
[
x
k
−
1
;
x
k
]
.
(15)
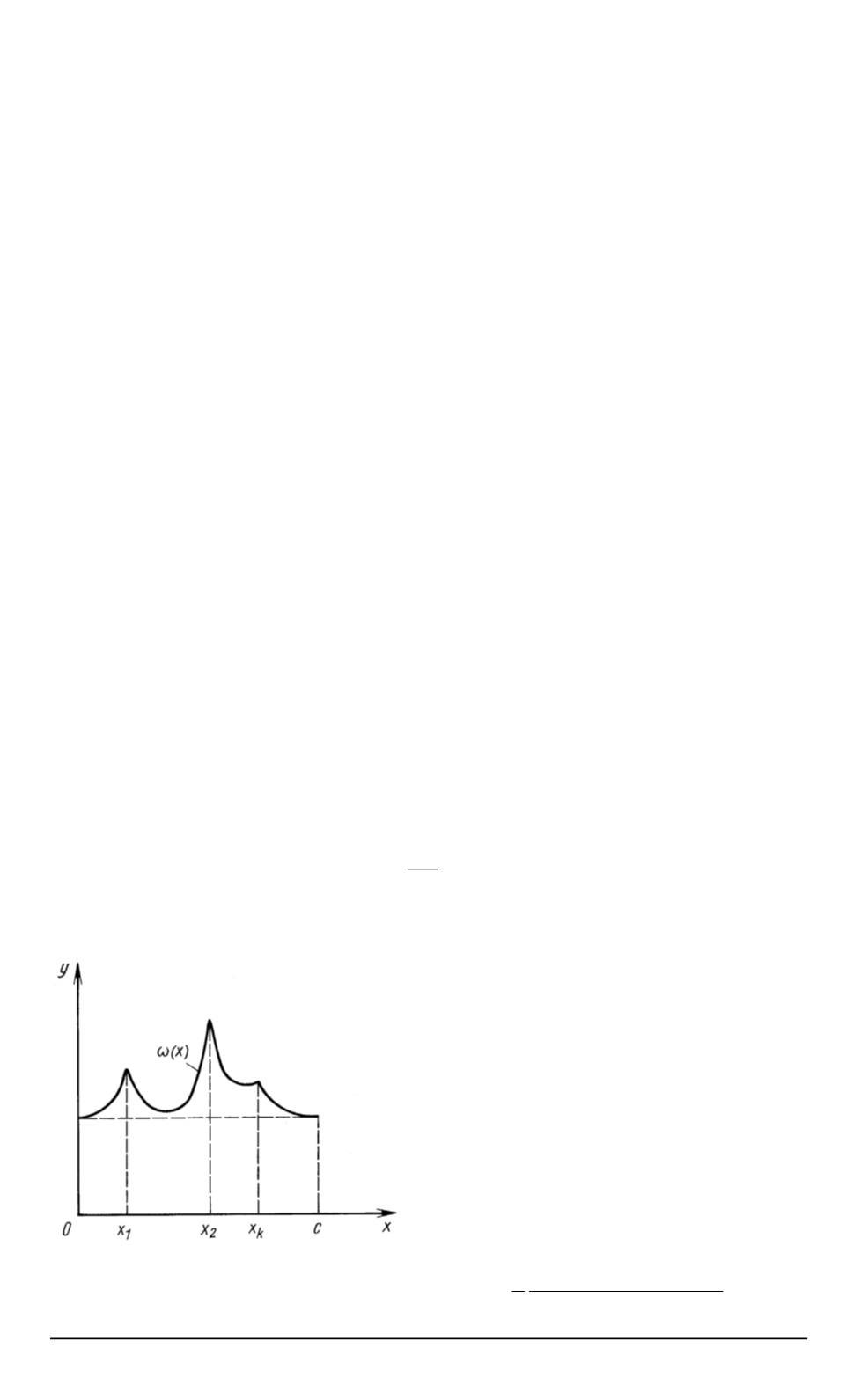
Рис
. 3.
Функция
ω
(
x
)
Потребуем также выполнения
условия
ω
k
(
x
k
) =
ω
k
+1
(
x
k
)
(16)
для всех
k
(
рис
. 3).
Тогда функция
p
(
x
)
будет выражаться через
ω
(
x
)
формально так же
,
как в форму
-
ле
(8),
но в терминах обобщенных
функций
.
Легко убедиться
,
что
p
(
x
)
будет иметь вид
(12),
где
m
k
=
−
1
2
ω
0
k
+1
(
x
k
)
−
ω
0
k
(
x
k
)
ω
(
x
k
)
.
(17)
18
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2


