Постоянные
κ
s
, s
= 0
,
3
,
выбираются таким образом
,
чтобы
z
1
=
=
z
2
=
z
3
=
z
4
= 0
было асимптотически устойчивым решением за
-
мкнутой системы
.
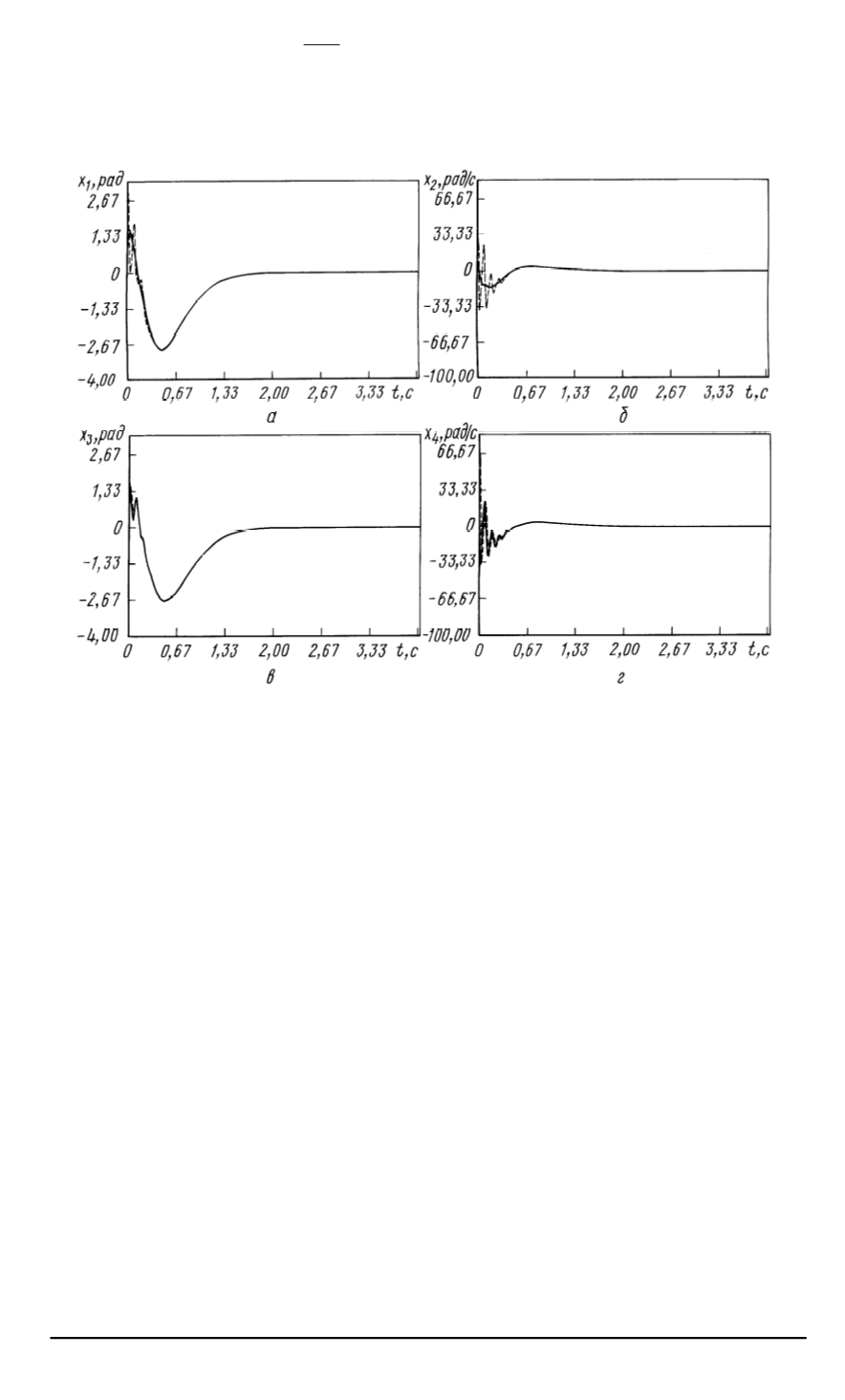
Переходные процессы системы
(
сплошные кривые
)
и наблюдателя
(
штриховые
кривые
)
для
x
1
(
а
)
,
x
2
(
б
)
,
x
3
(
в
)
,
x
4
(
г
)
Как уже отмечалось
,
из глобальной экспоненциальной устойчиво
-
сти положения равновесия системы
(43),
замкнутой управлением
(44),
следует глобальная экспоненциальная устойчивость соответствующе
-
го положения равновесия
x
= 0
,
u
= 0
системы
(37),
замкнутой упра
-
влением
u
(
x
) =
u
∗
(
µ
−
1
(
x
))
.
Следовательно
,
согласно теореме
3
упра
-
вление
u
(ˆ
x
) =
u
∗
(
µ
−
1
(ˆ
x
))
,
где
ˆ
x
—
оценка вектора состояния системы
(37),
получаемая с помощью наблюдателя
(41),
будет глобально асимп
-
тотически стабилизировать положение равновесия
x
= 0
,
u
= 0
систе
-
мы
(37).
Замечание
.
Глобальный экспонециальный наблюдатель для систе
-
мы
(37)
можно построить также
,
например
,
в виде
(9)
или
(11).
Результаты численного моделирования систем
(37)
и
(41)
с упра
-
влением
u
=
u
∗
(
µ
−
1
(ˆ
x
))
представлены на рисунке для следующих
значений параметров и начальных данных рассматриваемой системы
и наблюдателя
:
M
1
= 26
рад
·
c
−
2
;
k
1
= 230
c
−
2
;
k
2
= 1783
c
−
2
;
b
1
= 1
,
75
c
−
1
;
J
= 0
,
004
кг
·
м
2
;
θ
= 50
;
(
x
1
(0)
, x
2
(0)
, x
3
(0)
, x
4
(0))
т
=
= (1
,
5; 0
,
02; 1
,
41; 0
,
01)
т
;
(ˆ
x
1
(0)
,
ˆ
x
2
(0)
,
ˆ
x
3
(0)
,
ˆ
x
4
(0))
т
= (0
,
0
,
0
,
0)
т
.
58
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2


