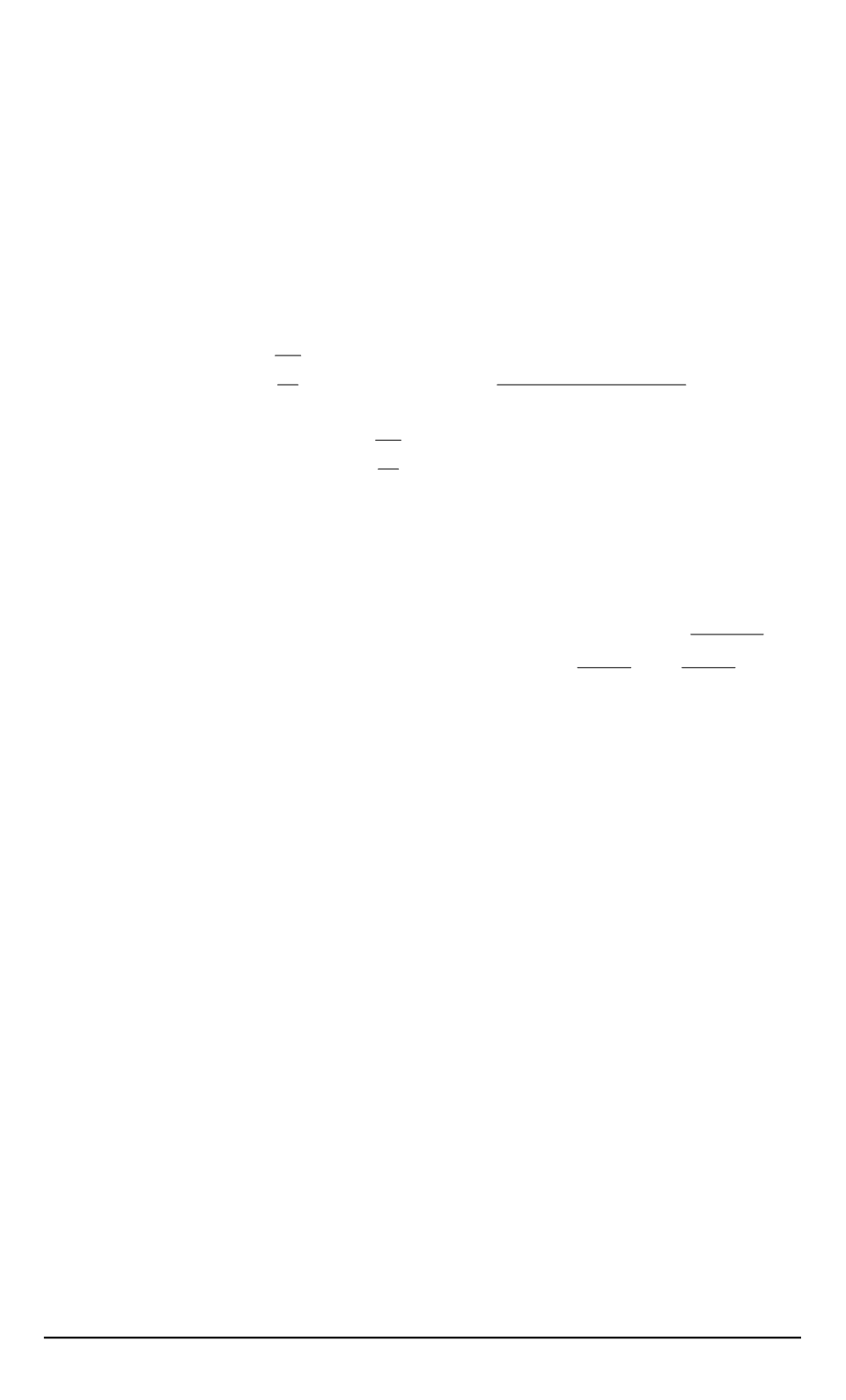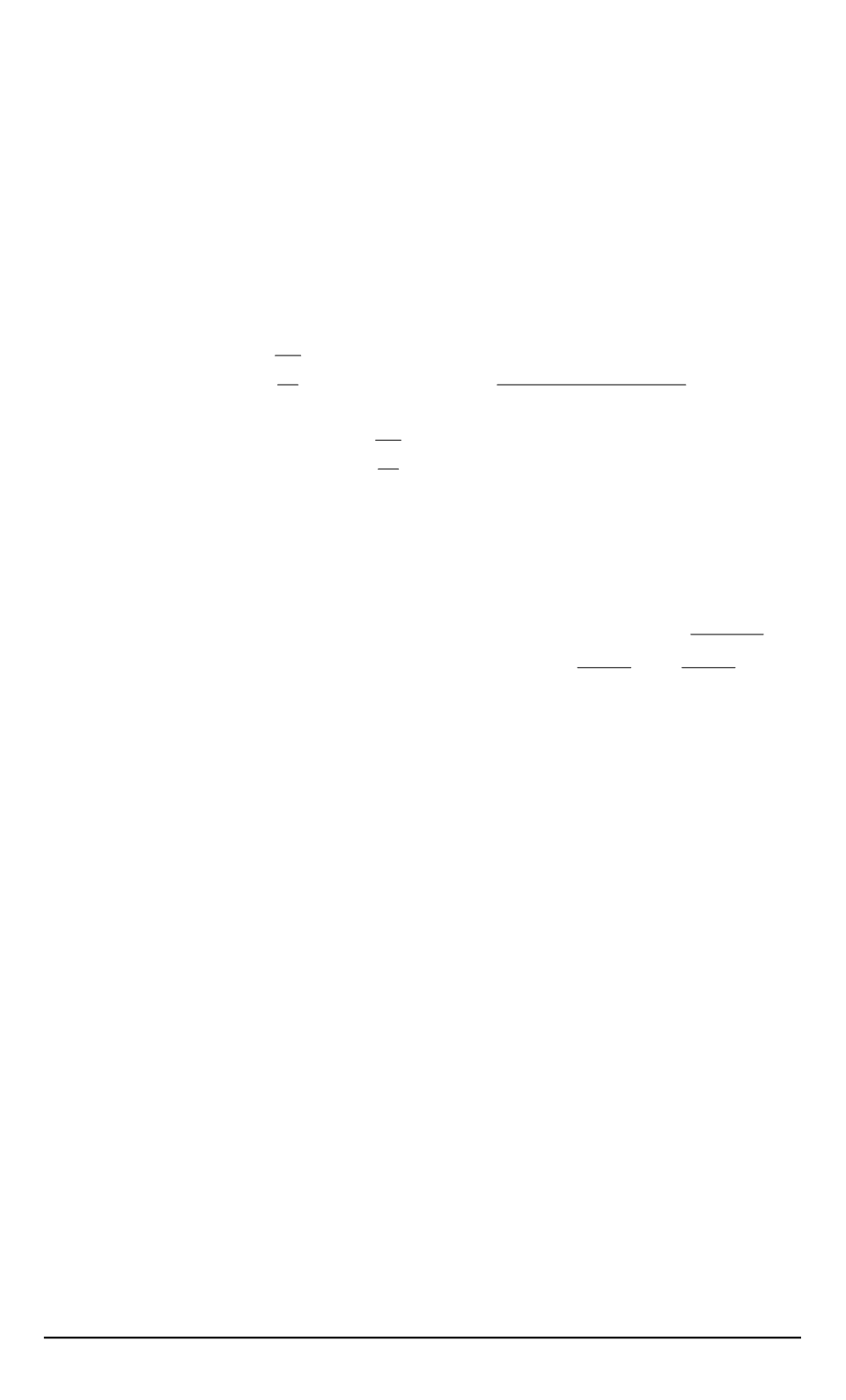
системы
(21)
с данным управлением
u
=
u
(
x
+
e
)
определено при всех
t
≥
0
.
Тогда в силу замены переменных
(26)
для любых
ˆ
x
(0)
решения
ˆ
x
(
t
)
системы
(35)
также определены при всех
t
≥
0
.
Из неравенств
(36)
и
(24) (
с учетом замены
x
на
ˆ
x
)
следует
,
что со
-
гласно работе
[18]
система
(35)
обладает устойчивостью отображения
вход
–
состояние по отношению ко входу
е
,
генерируемому системой
(21)
с управлением
u
=
u
(
x
+
e
)
,
и можно показать аналогично тому
,
как это сделано в работе
[18],
что для любого
ˆ
x
(0)
и любого решения
e
(
t
)
системы
(21)
с управлением
u
=
u
(
x
+
e
)
решение
ˆ
x
(
t
)
системы
(35)
при всех
t
≥
0
удовлетворяет неравенству
|
ˆ
x
(
t
)
−
x
∗
| ≤
r
c
2
c
1
|
ˆ
x
(0)
−
x
∗
|
exp
µ
−
kc
4
−
c
3
γ
f
−
c
3
γ
F
2
kc
2
t
¶
+
+
k
r
c
2
c
1
sup
0
≤
τ
≤
t
|
e
(
τ
)
|
.
Воспользовавшись соотношениями
(26)
и неравенствами
|
x
−
x
∗
+
+
e
| ≥ |
x
−
x
∗
| − |
e
|
и
|
x
−
x
∗
+
e
| ≤ |
x
−
x
∗
|
+
|
e
| ∀
(
x
−
x
∗
)
∈
R
n
,
∀
e
∈
R
n
,
получаем
,
что для любого
x
(0)
решение
x
(
t
)
системы
(1)
при управлении
u
=
u
(
x
+
e
)
,
где
u
(
x
)
соответствует формулировке
теоремы
3,
удовлетворяет неравенству
(34),
где
β
(
s, t
) =
p
(
c
2
/c
1
)
s
×
×
exp(
−
(
kc
4
−
c
3
γ
f
−
c
3
γ
F
)
/
(2
kc
2
)
t
)
,
α
(
s
) = (
k
p
c
2
/c
1
+
p
c
2
/c
1
+1)
s
,
s
∈
R
+
,
что завершает доказательство утверждения
.
Отметим
,
что часто удается достичь экспоненциальной устойчиво
-
сти замкнутой системы в одних переменных
,
а построить экспоненци
-
альный наблюдатель для системы
,
записанной в других переменных
.
В связи с рассматриваемой задачей стабилизации отметим следующие
два свойства преобразованной системы
.
Если две динамические систе
-
мы
˙
ξ
=
f
1
(
ξ, t
)
и
˙
η
=
f
2
(
η, t
)
связаны заменой переменных
ξ
=
H
(
η
)
,
где
H
—
диффеоморфизм пространств
R
n
=
{
η
}
и
R
n
=
{
ξ
}
,
то гло
-
бальная асимптотическая устойчивость положения равновесия
ξ
∗
пер
-
вой системы эквивалентна глобальной асимптотической устойчивости
соответствующего положения равновесия
η
∗
=
H
−
1
(
ξ
∗
)
второй систе
-
мы
.
Если же отображения
H
и
H
−
1
,
к тому же
,
глобально липшицевы
(
например
,
это линейные отображения
),
то аналогичное утверждение
верно для глобальной экспоненциальной устойчивости этих положе
-
ний равновесия
.
Последнее следует из неравенств
|
η
(
t
)
−
η
∗
|
=
|
H
−
1
(
ξ
(
t
))
−
H
−
1
(
ξ
∗
)
| ≤
≤
γ
1
|
ξ
(
t
)
−
ξ
∗
| ≤
γ
1
β
exp(
−
αt
)
|
ξ
(0)
−
ξ
∗
|
=
=
γ
1
β
exp(
−
αt
)
|
H
(
η
(0))
−
H
(
η
∗
)
| ≤
γ
1
γ
2
β
exp(
−
αt
)
|
η
(0)
−
η
∗
|
,
где
β
,
α
,
γ
1
,
γ
2
—
соответствующие положительные константы
.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2
53