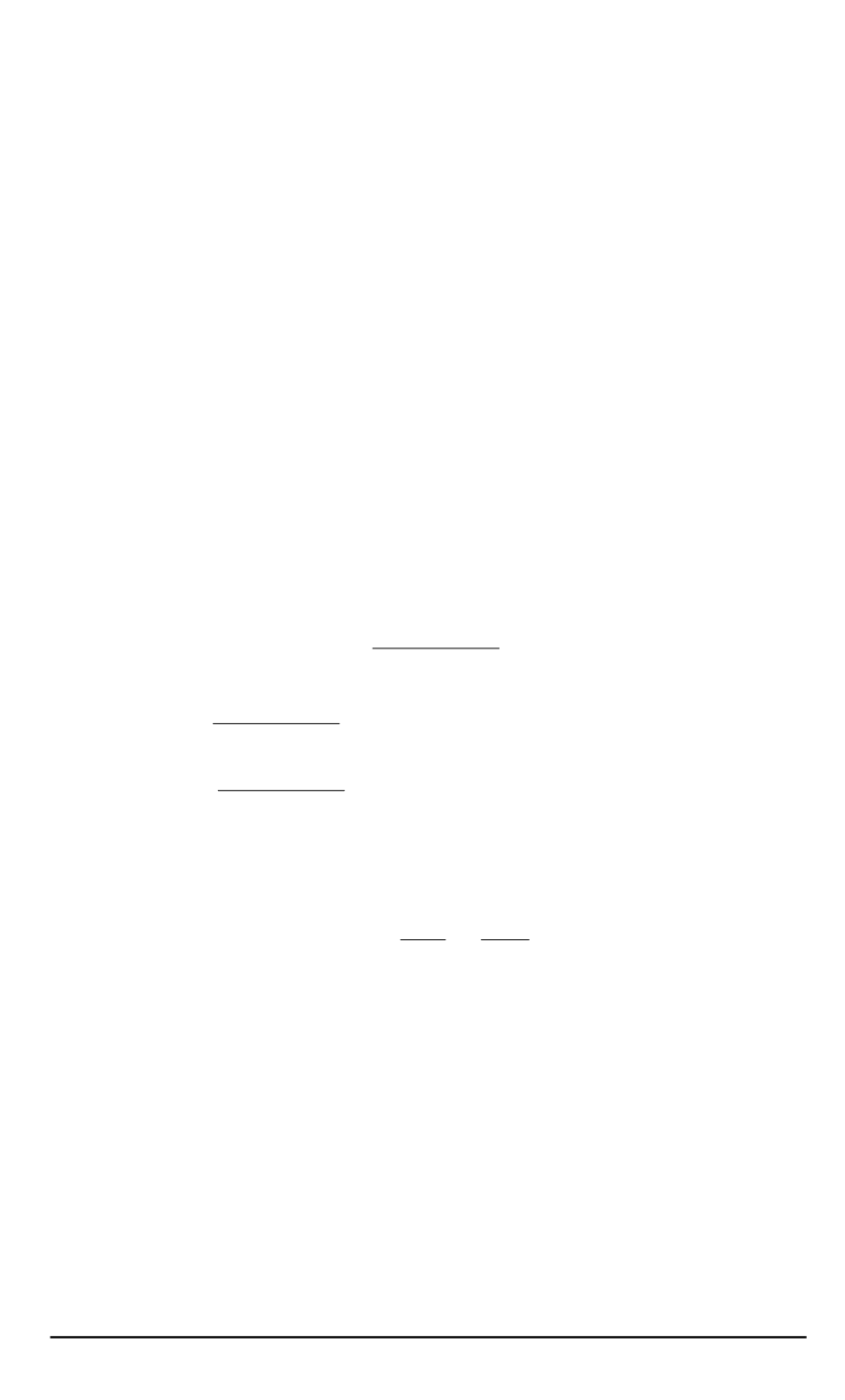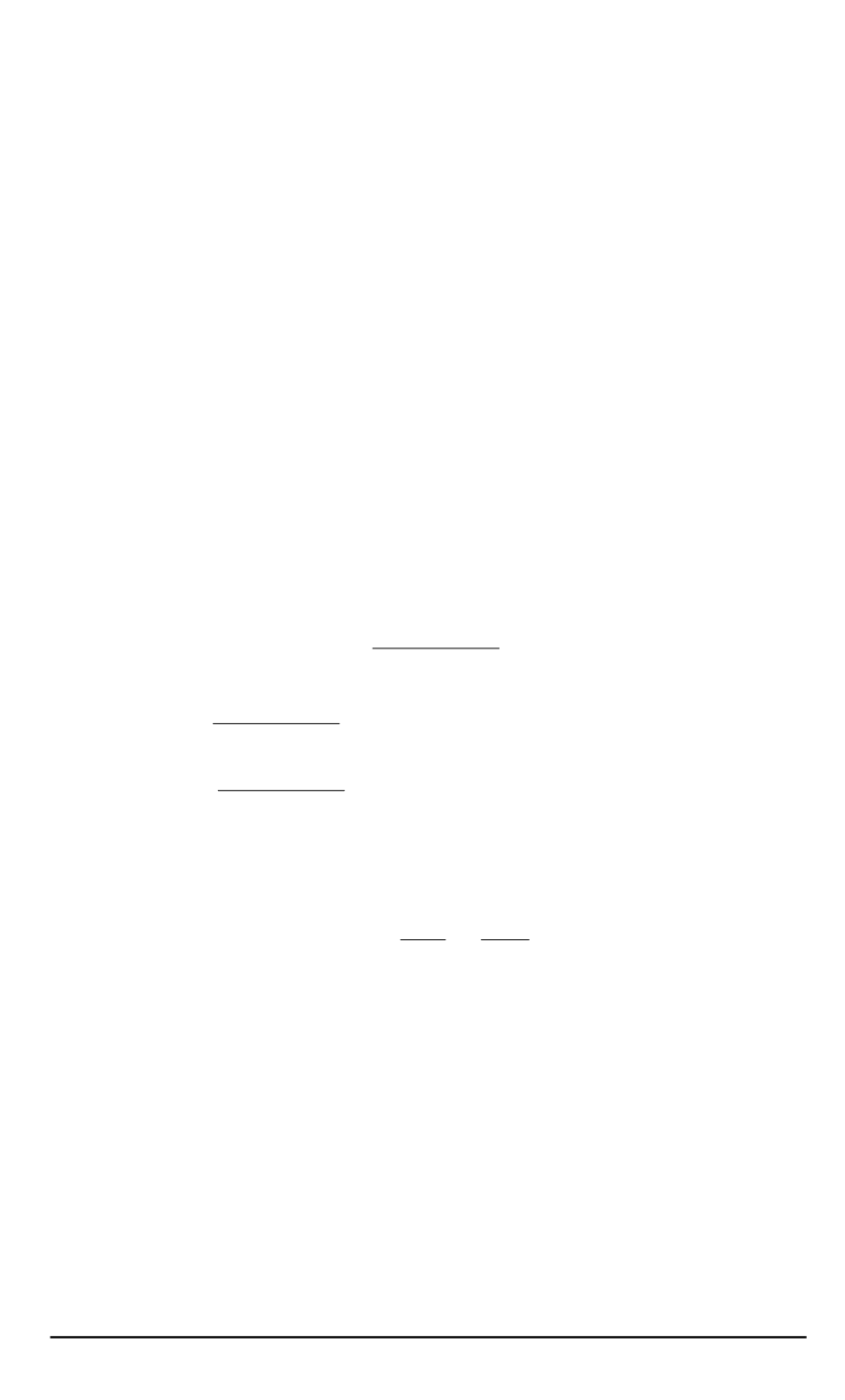
где
β
(
s, t
)
и
α
(
s
)
—
некоторые непрерывные функции своих аргумен
-
тов
,
строго возрастающие по
s
∈
R
+
,
α
(0) = 0
,
β
(0
, t
) = 0
∀
t
≥
0
,
причем имеем
β
(
s, t
)
→ ∞
при
s
→ ∞
для любого фиксированного
t
≥
0
,
а для любого фиксированного
s
∈
R
+
имеем
β
(
s, t
)
→
0
при
t
→ ∞
.
Доказательство
.
Рассмотрим систему
(23).
Линейная замена пере
-
менных
(26)
преобразует систему
(23)
к виду
(27).
Подсистема уравне
-
ний относительно
ˆ
x
системы
(27)
имеет вид
˙ˆ
x
=
f
(ˆ
x
−
e, u
(ˆ
x
)) +
F
(
e, u
(ˆ
x
)
, t
) = ˜
f
(ˆ
x, e
)
.
(35)
Отметим
,
что правая часть системы
(35)
явно от времени не зависит
,
так как согласно предположению
2
имеет вид
˜
f
(ˆ
x, e
) =
g
(ˆ
x, h
(ˆ
x
−
e
)
,
u
(ˆ
x
))
.
В качестве функции Ляпунова для системы
(35)
с возмущением
e
рассмотрим функцию
V
(ˆ
x
−
x
∗
) =
V
1
(ˆ
x
−
x
∗
)
,
где
V
1
(
x
−
x
∗
)
—
функция
Ляпунова для системы
(1),
замкнутой управлением
u
(
x
)
,
удовлетворя
-
ющая неравенствам
(24)
и
(25).
Произведя в неравенствах
(24), (25)
за
-
мену
x
на
ˆ
x
,
с учетом полученных неравенств производную
˙
V
в силу
системы
(35)
можно записать следующим образом
:
˙
V
(ˆ
x
−
x
∗
) =
∂V
1
(ˆ
x
−
x
∗
)
∂
ˆ
x
f
(ˆ
x, u
(ˆ
x
))+
+
∂V
1
(ˆ
x
−
x
∗
)
∂
ˆ
x
(
f
(ˆ
x
−
e, u
(ˆ
x
))
−
f
(ˆ
x, u
(ˆ
x
)))+
+
∂V
1
(ˆ
x
−
x
∗
)
∂
ˆ
x
F
(
e, u
(ˆ
x
)
, t
)
≤ −
c
4
|
ˆ
x
−
x
∗
|
2
+
+(
c
3
γ
f
+
c
3
γ
F
)
|
e
||
ˆ
x
−
x
∗
|
.
При
|
ˆ
x
−
x
∗
| ≥
k
|
e
|
,
k >
0
,
справедлива следующая оценка
:
˙
V
(ˆ
x
−
x
∗
)
≤ −
³
c
4
−
c
3
γ
f
k
−
c
3
γ
F
k
´
|
ˆ
x
−
x
∗
|
2
≤
0
(36)
при
k >
(
c
3
γ
f
+
c
3
γ
F
)
/c
4
.
C
огласно предположению
2
любое решение
e
(
t
)
системы
˙
e
=
F
(
e,
u
(
x
+
e
)
, t
)
определено по крайней мере на некотором конечном ин
-
тервале времени
t
∈
[0
, T
)
,
T >
0
,
и на этом интервале непрерывно и
ограничено
.
Неравенства
(36)
и
(24) (
с учетом замены
x
на
ˆ
x
)
означа
-
ют
,
что при любых
ˆ
x
(0)
любому ограниченному возмущению
e
(
t
)
со
-
ответствует ограниченное решение
ˆ
x
(
t
)
системы
(1)
и
,
следовательно
,
ограниченное решение
x
(
t
)
системы
(1)
с управлением
u
=
u
(
x
+
e
)
,
где
u
(
x
)
соответствует формулировке теоремы
3.
Следовательно
,
для
любых начальных значений
x
(0)
решения
x
(
t
)
системы
(1) c
управле
-
нием
u
=
u
(
x
+
e
)
определены при всех
t
≥
0
,
и любое решение
e
(
t
)
52
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2