конуса равен 7
◦
, радиус затупления 0,0127 м, температура поверхно-
сти тела 300 K. Число Рейнольдса для данного режима
12
,
1
∙
10
6
м
−
1
.
График зависимости числа Стантона (безразмерный тепловой по-
ток) от координаты, отсчитываемой от носка тела вдоль оси конуса
приведен на рис. 7, причем число Стантона определяется по формуле
St
=
q
w
ρ
∞
V
∞
(
h
(
T
r
)
−
h
w
)
,
где
q
w
— тепловой поток;
h
w
— энтальпия газа на стенке;
h
(
T
r
)
—
энтальпия газа в пограничном слое, соответствующая температуре
восстановления
T
r
=
T
∞
1 +
r
γ
−
1
2
M
2
∞
. Коэффициент восстано-
вления
r
для ламинарного слоя принимается равным 0,85, для турбу-
лентного — 0,89.
Для турбулентных режимов обтекания, как было ранее отмечено,
в области критической точки тепловой поток близок к потоку при
ламинарном течении, а при смещении вдоль сферы на центральный
угол 30
◦
и более ведет к превышению значений теплового потока
при турбулентном обтекании по отношению к тепловому потоку при
ламинарном течении.
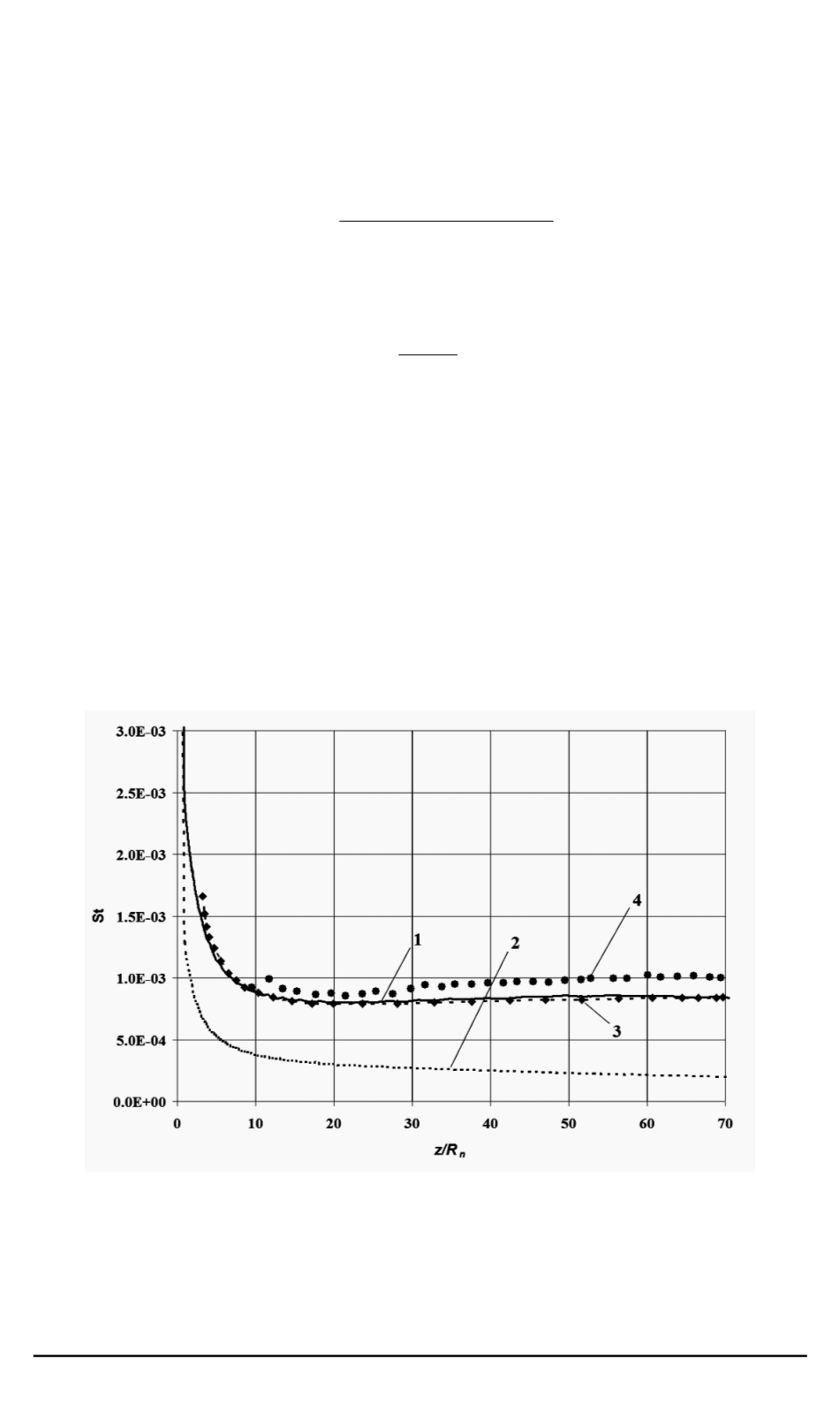
На рис. 7 показано качественное различие в распределении тепло-
вых потоков вдоль поверхности тела. Так, для турбулентного погра-
Рис. 7. Распределение числа Стантона (безразмерный тепловой поток) в
зависимости от координаты, отсчитываемой от носка тела вдоль оси конуса:
M
∞
= 8
, Re
∞
= 12
,
1
∙
10
6
м
−
1
;
1
— расчет для случая турбулентного обтекания
по модели настоящей работы;
2
— расчет для случая ламинарного обтекания;
3
—
расчет для случая турбулентного обтекания по модели Себечи–Смита [7];
4
—
экспериментальные данные для случая турбулентного обтекания [7]
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1
101


