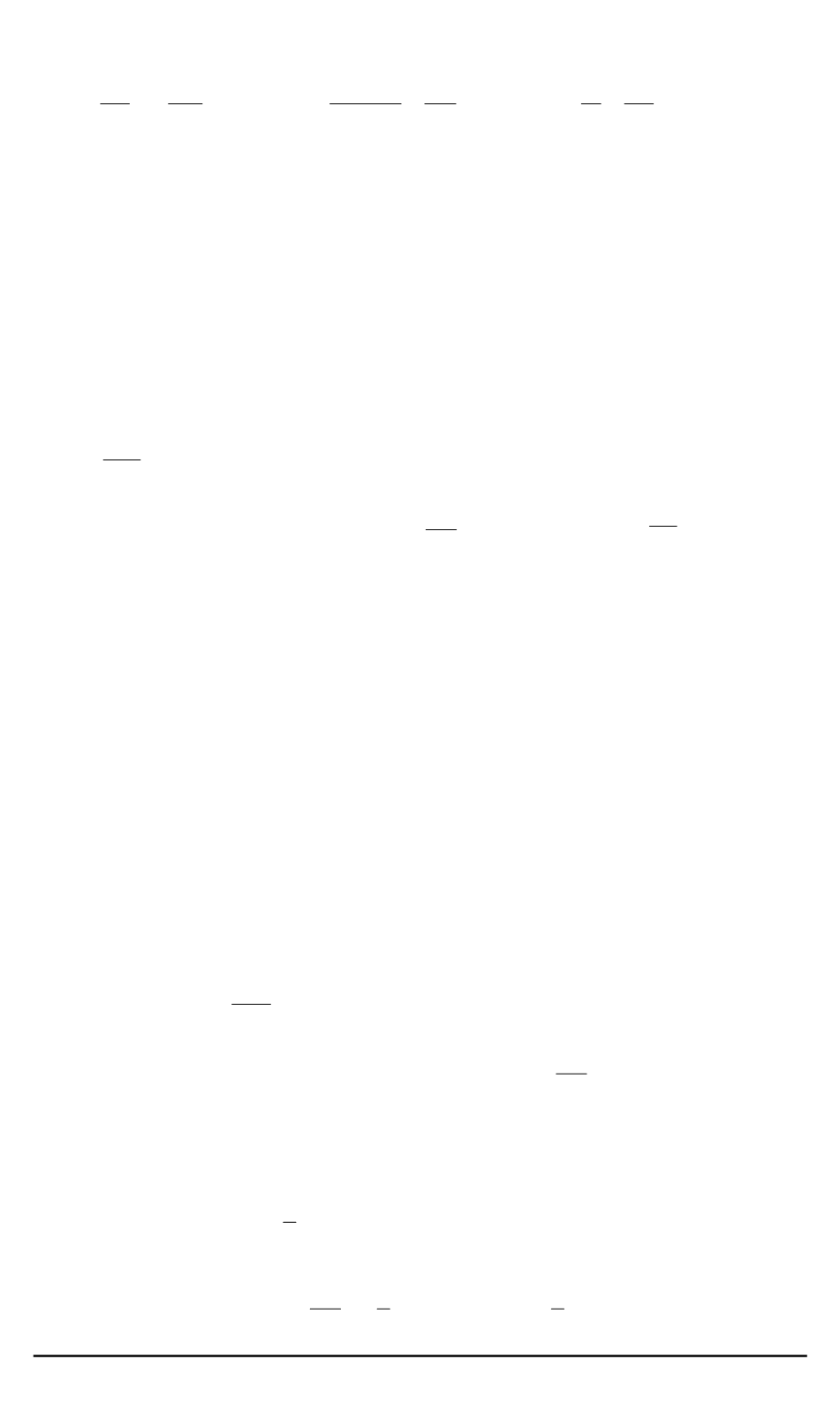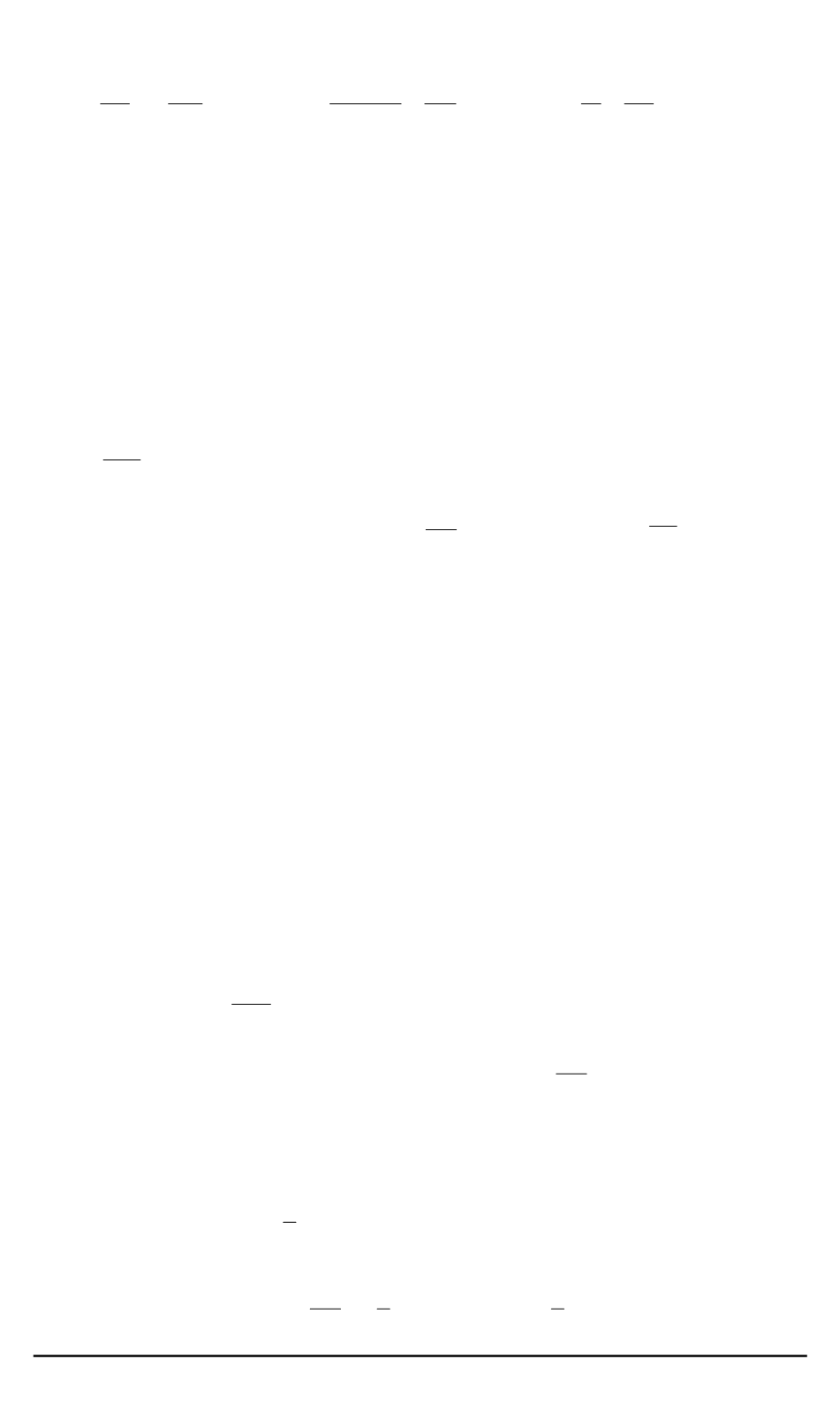
— по касательному направлению и
∂u
∂y
=
∂u
∂R
(
~e
R
∙
~e
y
) +
1
R
sin
θ
∙
∂u
∂ϕ
(
~e
ϕ
∙
~e
y
) +
1
R
∙
∂u
∂θ
(
~e
θ
∙
~e
y
)
— по нормали.
Описание численной схемы.
На основе расщепления задачи обте-
кания по физическим процессам используется численный метод, опи-
санный в работе [3].
Этап 1
. Интегрируется “невязкая” часть системы, включающая в
себя уравнения движения Эйлера, неразрывности и энергии только с
невязкими членами:
ρ
d
→
U
dt
=
→
K,
где
~U
=
ρ
→
V
h
+
V
2
2
, ~K
=
−
ρ
2
div
~V
−
grad
p
∂p
∂t
.
“Невязкая” часть газодинамической системы уравнений решается с
использованием явной двухшаговой конечно-разностной схемы Мак-
Кормака.
Введем в пространстве
t, ξ, ϕ, θ
сетку с шагами
Δ
t,
Δ
ξ
,
Δ
ϕ
=
π
/
K,
Δ
θ
и обозначим координаты узлов сетки как
t
j
=
j
Δ
t
,
θ
m
=
m
Δ
θ, ϕ
k
=
k
Δ
ϕ
, а любую функцию
f
в точке как
f
j
n,m,k
. При
этом
0
6
n
6
N
,
0
6
m
6
M
,
0
6
k
6
K
, где
N, M, K
— число
интервалов в направлениях
ξ, θ, ϕ
соответственно.
Этап 2
. Решение уточняется с использованием “вязкой” части
уравнений Навье–Стокса и энергии:
ρ
∂
→
U
∂t
=
→
K,
где
~U
=
ρ
→
V
h
+
V
2
2
,
~K
=
0
−
2
3
grad
μ
div
→
V
+ 2Div
μ
.
S
div
2
μ
grad
V
2
2
−
1
2
→
V
×
rot
→
V
−
2
3
μ
→
V
div
→
V
−
~q
.
96
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1