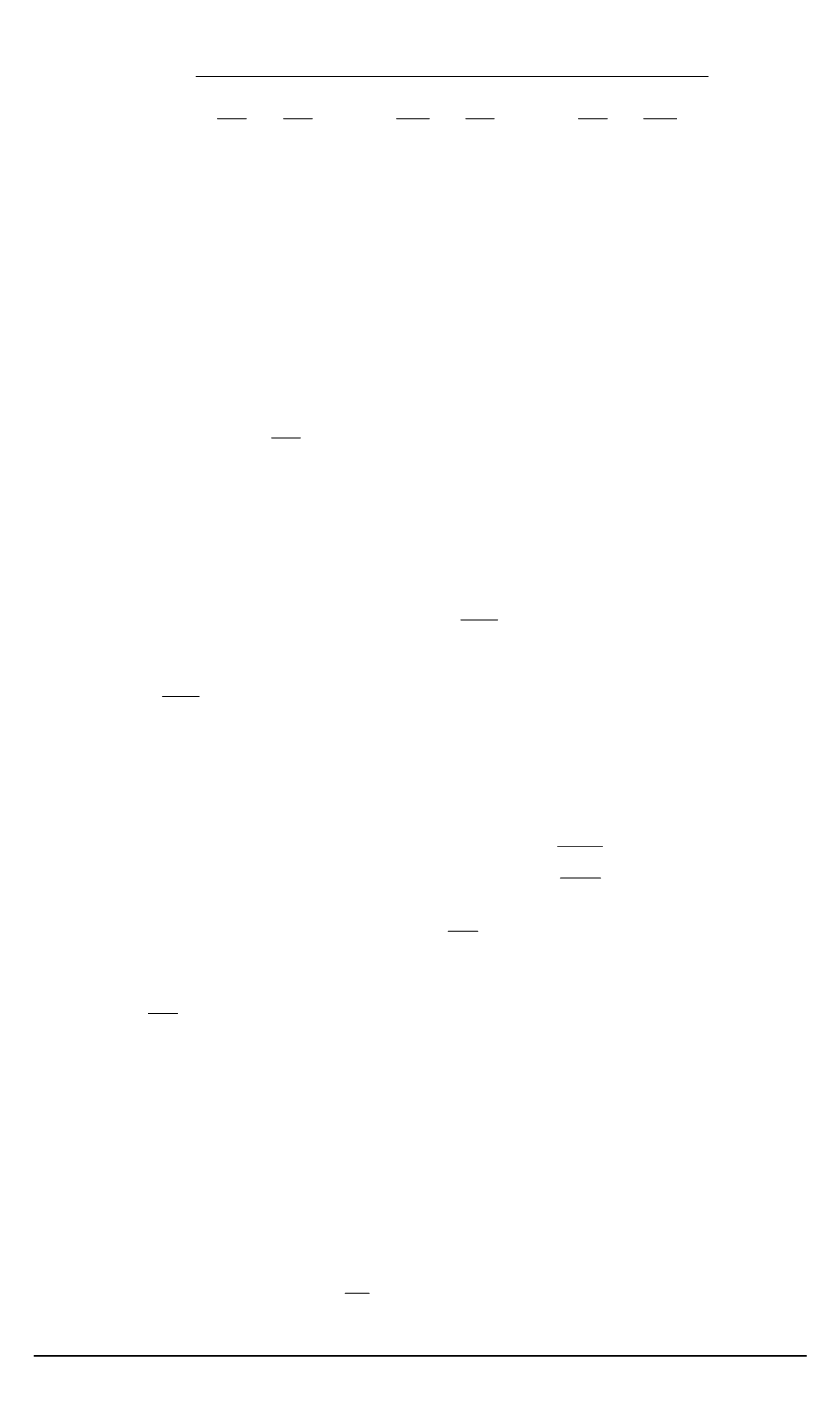
завихренности:
s
=
s
∂v
∂x
−
∂u
∂y
2
+
∂w
∂y
−
∂v
∂z
2
+
∂u
∂z
−
∂w
∂x
2
;
l
— величина, пропорциональная длине пути смешения (расстояние
в поперечном направлении, на котором частицы еще сохраняют свой
собственный импульс) и зависящая от типа рассматриваемого течения
(пограничный слой, струя, след и т.п.);
u, w
— компоненты скорости в
направлении основного течения,
v
— в поперечном направлении;
x, y
— продольная и поперечная координаты.
Турбулентная вязкость рассматривается как скаляр, что дает каче-
ственно правильные результаты, особенно для пристеночных течений
[1]. Произведение
l
∂u
∂y
можно интерпретировать как характерную
скорость турбулентности
v
т
.
При вычислении
l
для внутренней области, расположенной в не-
посредственной близости от стенки, хорошие результаты дает оценка
согласно формуле [1]
l
=
χy
1
−
e
−
y
+
A
.
(2)
Здесь
1
−
e
−
y
+
A
— демпфирующая функция Ван-Дриста, необходимая
для связи между полностью развитым пограничным слоем (
l
=
χy
) и
вязким подслоем (
l
→
0
);
χ
= 0
,
41
— постоянная Кармана;
A
= 26
—
демпфирующая константа;
y
+
=
u
T
y/ν
w
— сеточный параметр, ха-
рактеризующий качество сетки в пристеночной области течения и
являющийся безразмерной величиной;
u
T
=
r
|
τ
w
|
ρ
w
— постоянная для
луча динамическая скорость;
ν
w
=
μ
w
ρ
w
— кинематическая вязкость;
μ
w
— динамическая вязкость;
ρ
w
— плотность на поверхности тела;
τ
w
=
μ
w
∂u
∂y
w
— касательное напряжение трения; индекс
w
соответ-
ствует параметрам на стенке.
Для расчета турбулентной вязкости во внешней области погранич-
ного слоя используется формула Клаузера [1]
μ
т
=
αρδ
i
u
e
/I,
где
u
e
— скорость на границе пограничного слоя; параметр
α
≈
0
,
0168
(его модификация позволяет учитывать эффекты при малых числах
Рейнольдса);
δ
i
=
δ
Z
0
1
−
u
u
e
dy
— толщина вытеснения;
I
= 1 +
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1
91