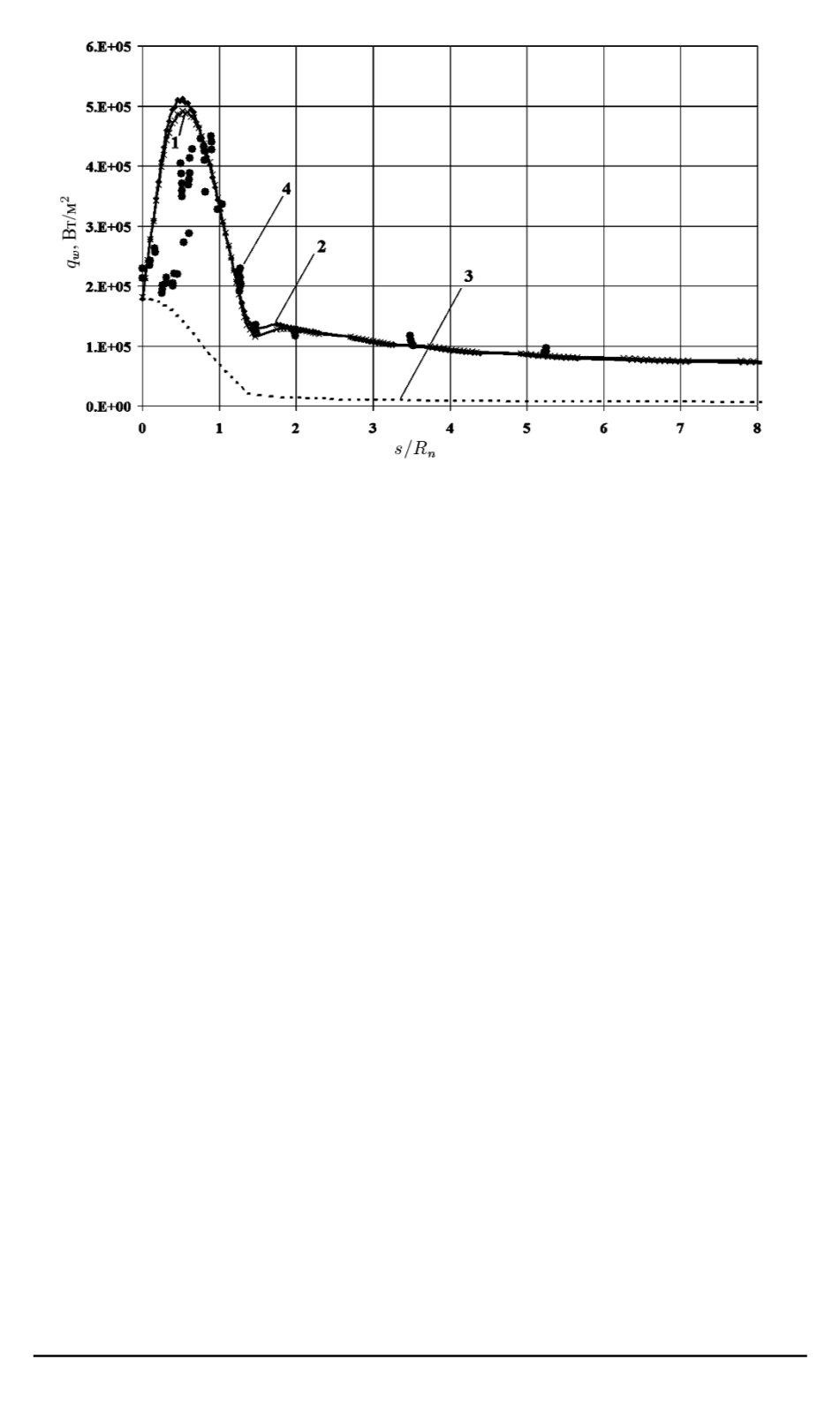
Рис. 6. Распределение размерного теплового потока по длине образующей тела:
M
∞
= 5
, Re
∞
= 60
∙
10
6
м
−
1
;
1, 2
— расчет для случая турбулентного обтекания,
соответственно сетка 1 и 2;
3
— расчет для случая ламинарного обтекания;
4
—
экспериментальные данные для случая турбулентного обтекания [6, 7]
сетки и начального приближения, что сравнимо с затратами на по-
лучение полного решения с использованием коммерческих пакетов.
Отметим, однако, что применение коммерческих программных ком-
плексов также требует тщательного сравнения полученных решений
с экспериментальными данными. Кроме того, при их использовании
отсутствует возможность модификации применяемых математических
моделей, что ставит исследователей в зависимость от разработчиков
коммерческих программ.
Анализируя результаты расчетов (рис. 6), можно отметить, что раз-
витая турбулентность наступает уже на сфере на расстоянии примерно
0,6 калибра по длине образующей
s
(расстояние вдоль поверхности те-
ла), в этом месте заметно резкое увеличение теплового потока (до 2,5
раз) по сравнению с критической точкой. В целом можно отметить
удовлетворительное согласование (различия не превышают 30%) рас-
четных и экспериментальных данных, учитывая погрешность экспе-
римента в пределах 10–20%. Здесь же приведены результаты расчета
теплового потока в ламинарном режиме (нижняя кривая). Сравнение
показывает, что турбулентный тепловой поток намного превышает ла-
минарный, а его максимум смещается по потоку от точки торможения.
Изменение числа узлов поперек ударного слоя не приводит к за-
метному изменению значения теплового потока, что позволяет сделать
вывод о правильном выборе расчетной сетки.
Для второго рассмотренного режима число Маха задавалось рав-
ным 8, длина тела — 70 калибрам, угол полураствора затупленного
100
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1


