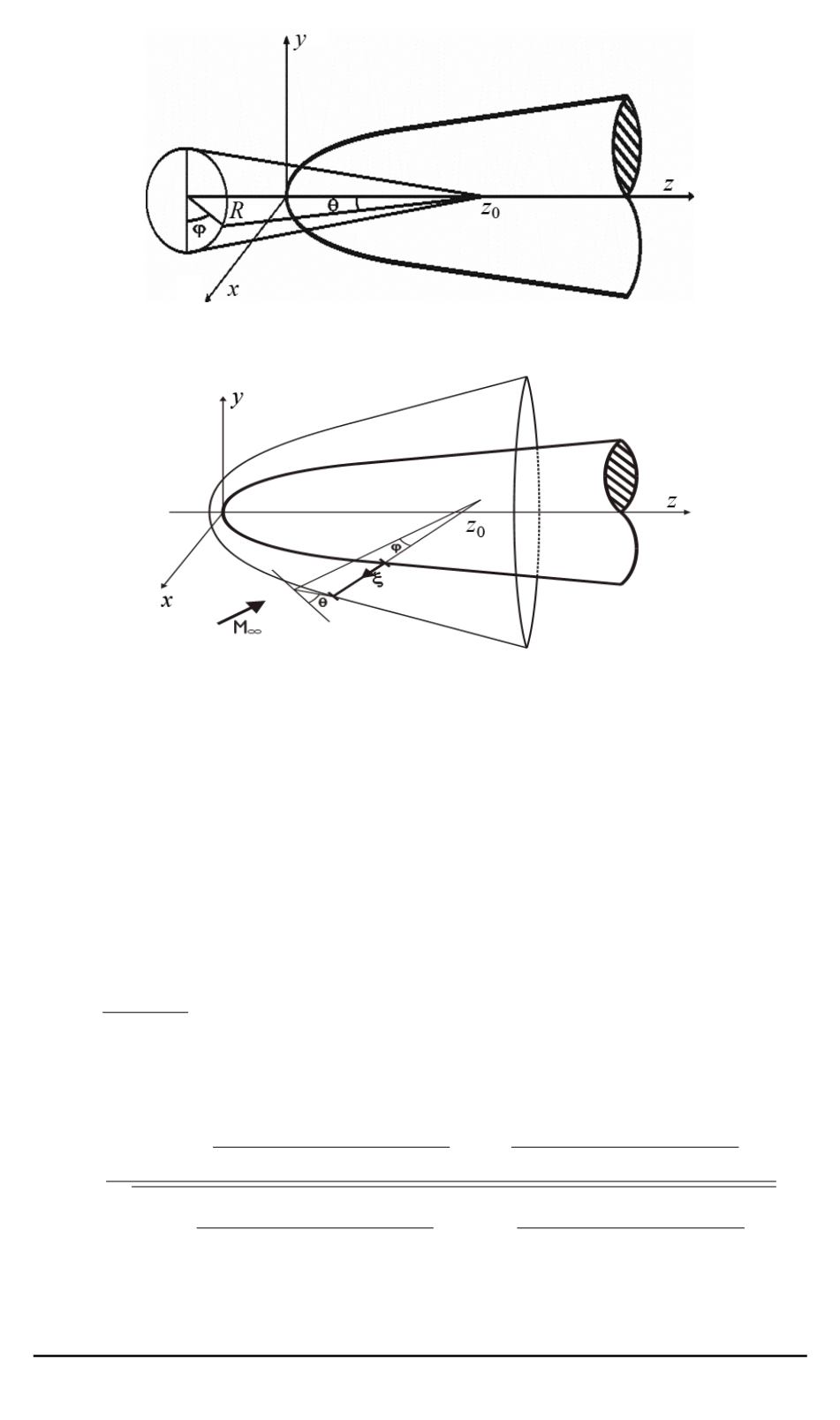
Рис. 2. Исходная сферическая система координат
Рис. 3. Нормированная сферическая система координат
волны соответственно, причем
R
B
определяется в процессе решения
задачи обтекания.
Расчет течений около затупленных тел будем проводить в норми-
рованной сферической системе координат
ξ
,
ϕ
,
θ
(рис. 3), полученной
из исходной ССК.
Определим преобразование компонент скорости из сферической
системы координат в локальную систему координат, связанную с об-
текаемым телом (рис. 4).
В локальной системе координат компоненты скорости определя-
ются соотношениями
v
=
~V
∙
~n
для нормальной составляющей и
u
=
√
V
2
−
v
2
для касательной составляющей.
Уравнение для нормали к поверхности
R
−
R
T
+
ξ
(
R
B
−
R
T
) = 0
в
нормированной сферической системе координат записывается в виде
~n
=
1;
−
R
Tϕ
+ (
R
Т
ϕ
−
R
Tϕ
)
ξ
R
sin
θ
;
−
R
T θ
+ (
R
Bθ
−
R
T θ
)
ξ
R
s
1 +
R
Tϕ
+ (
R
Т
ϕ
−
R
Tϕ
)
ξ
R
sin
θ
2
+
R
T θ
+ (
R
Bθ
−
R
T θ
)
ξ
R
2
;
нижние индексы
θ, ϕ
обозначают дифференцирование по соответству-
ющей переменной.
94
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1


