Формула оценивания регрессионного коэффициента нелинейной парной регрессии с использованием весовой функции - page 4

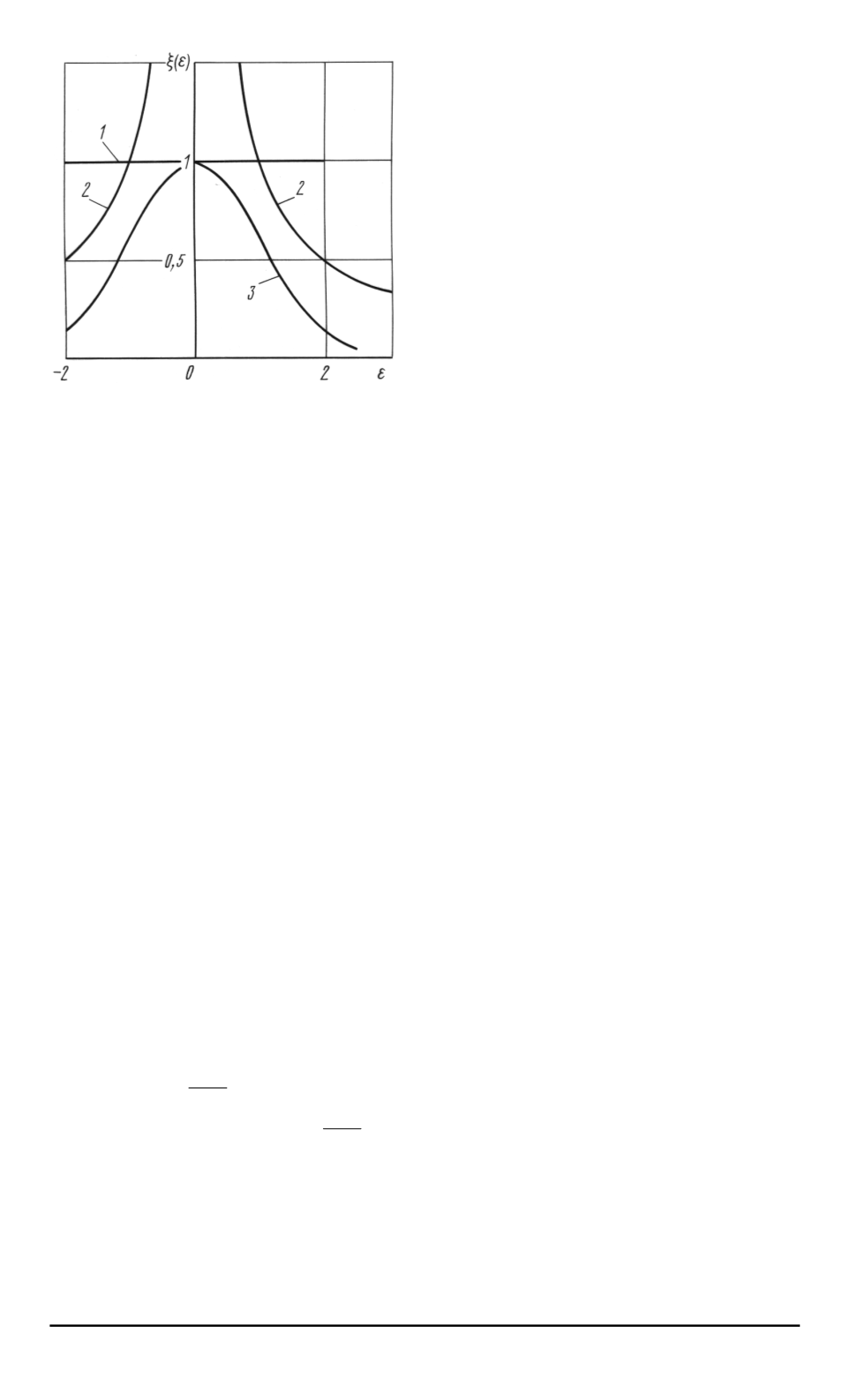
Рис. 1. Весовые функции регрессий:
1 — весовая функция ОНК
(ξ (ε) = 1); 2 — весовая функция
МО ( ξ(ε) = sign(ε)/ε); 3 — весовая
функция СОМ (ξ (ε) = e− λε2 /2 при
λ = 1)
Весовая функция регрес -
сии. Весовая функция связана с
оценочной функцией равенством
ξ(˜ε) = ˜ε −1 ψ(˜ε) . Построим графи -
ки весовых функций регрессии,
с точностью до ∂r ¡x, ˜
θ ¢/∂ ˜
θ со -
ответствующих оценочным функ-
циям ψ(˜ε ) = ˜ε , ψ(˜ε) = sign(˜ε) ,
ψ(˜ε ) = ˜ε e− λ˜ε2/2 , которые , в свою
очередь, соответствуют минималь -
но контрастным ОНК, МО и СОМ.
Предположим, что частная про -
изводная ∂r(x, θ ) /∂θ существует в
области ℵ × Θ определения функ -
ции r (x, θ ) и ограничена. Весовая
функция ОНК имеет вид ξ (˜ε ) = 1
(кривая 1 на рис. 1), в этом случае
все наблюдения имеют равные ве-
са. Весовая функция МО имеет вид ξ (˜ε ) = sign(˜ε ) / ˜ ε (кривая 2), в
этом случае наблюдения с большими отклонениями имеют малые ве-
са, а веса наблюдений с малыми отклонениями неограниченно возра -
стают. Анализ кривой 3 на рис. 1, соответствующей весовой функции
СОМ ξ (˜ε ) = e− λ˜ε2/2 при λ = 1, позволяет сделать вывод о том , что на-
блюдения с большими отклонениями имеют веса меньшие, чем в слу -
чае весовой функции МО, а веса наблюдений с малыми отклонениями
приближаются к единице. Таким образом , при малых отклонениях на -
блюдений значения, полученные с помощью весовой функции СОМ ,
приближаются к значениям, полученным с помощью весовой функции
ОНК, а при больших отклонениях — к полученным с помощью весовой
функции МО с усилением или ослаблением свойств МО в зависимости
от значений параметра λ.
Рекуррентная формула оценивания регрессионного коэффици -
ента. Обозначим ◦
θ = ¡ ◦
θ1 , ◦
θ2 , . . . , ◦
θ n ¢ значения регрессионного коэф -
фициента, реализующего функцию регрессии Y = r (X, θ) в точках
(xi, yi) , i = 1, n . Получить значения ◦
θi можно, решив систему урав -
нений yi = r ¡ xi, ◦
θi ¢, i = 1, n, относительно ◦
θ i. Отметим, что в общем
случае решение каждого из уравнений этой системы не является един-
ственным. На практике получить единственное решение можно , сузив
область возможных значений ◦
θi , исходя из условий конкретной зада-
чи [3]. Пусть
14 ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2004. № 4