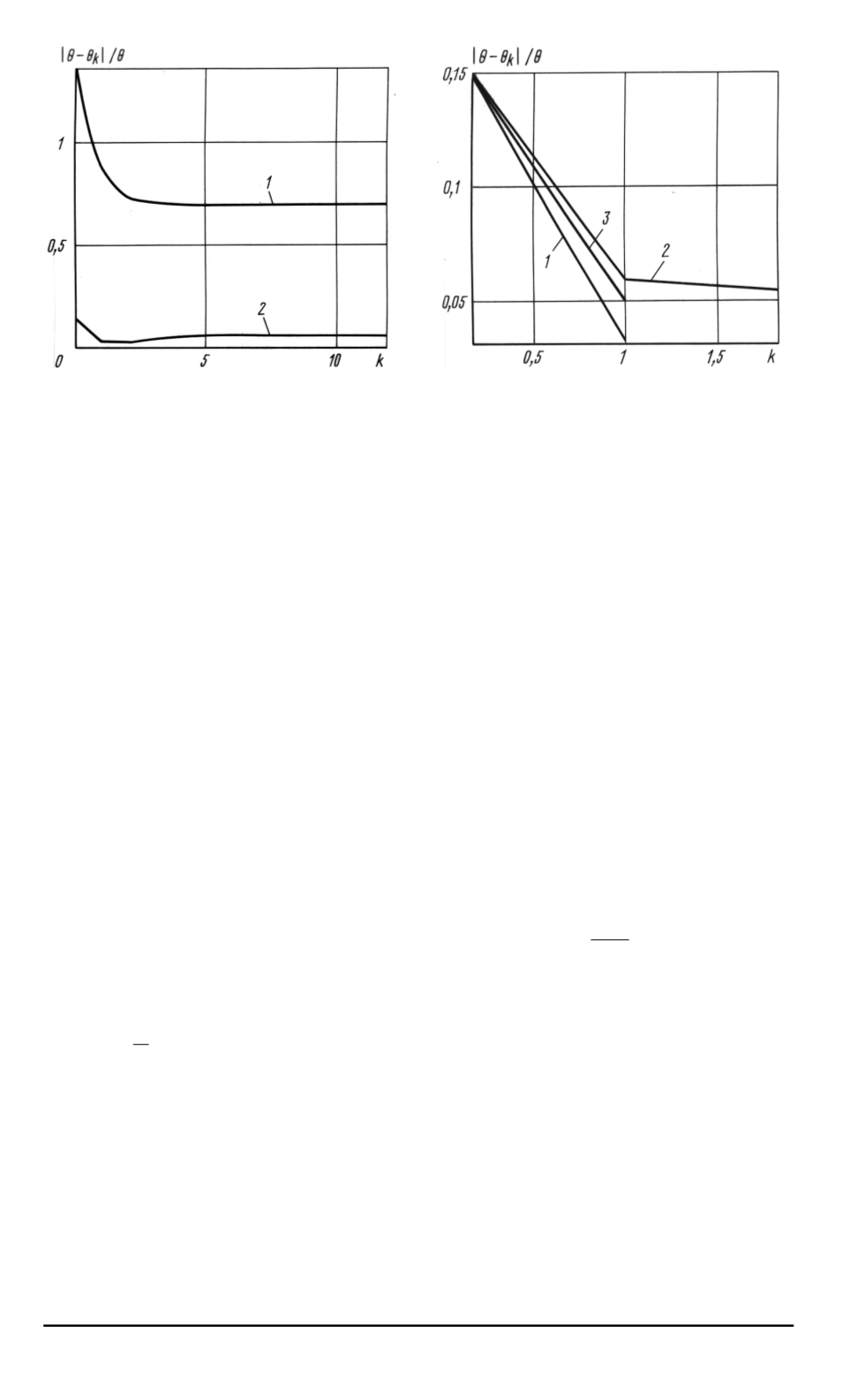
Рис
. 4.
Зависимость значений функ
-
ционала
(
1
)
и относительной погреш
-
ности
(
2
)
для случая использования
весовой функции МО
Рис
. 5.
Зависимость относительной
погрешности
|
θ
−
θ
k
|
/θ
оценки пара
-
метра
θ
от номера итерации
k
после
изменения условия конца итерации
для случаев использования весовых
функций МО
(
1
),
ОНК
(
2
)
СОМ
(
3
)
раметрам
.
Вследствие этого предлагаемый в настоящей работе метод
имеет преимущества перед существующим методом
,
программно обес
-
печенным в системе
Maple 7,
для класса парных нелинейных по пара
-
метру регрессий
.
Чтобы осуществить сравнение рассмотренных результатов с ре
-
зультатами оценивания
,
полученными с использованием программы
fit,
линеаризуем функцию регрессии
(6)
методом логарифмирования
:
ln(
Y
) = ln(
C
) +
X
3
θ
−
2
.
Введем обозначения
Z
:= ln(
Y
)
,
β
:=
θ
−
2
.
В результате получим
линейную по параметру
β
модель
Z
= ln(
C
) +
βX
3
.
Исходными дан
-
ными для программы
fit
являются точки
(
x
i
, z
i
)
,
i
= 1
, n
,
где
z
i
= ln(
y
i
)
.
Получим параметр
β
как результат аппроксимации
:
β
=
Z
(1)
−
ln(
C
)
.
Тогда оценка
˜˜
θ
искомого регрессионного коэффициента будет равна
˜
θ
= 1
/
√
β
.
В табл
. 1
приведены результаты оценивания по формуле
(5) (
столб
-
цы
˜
θ
MO
,
˜
θ
OHK
,
˜
θ
COM
)
и с использованием программы
fit (
столбец
˜˜
θ
),
из
которых видно
(
см
.
строки
1–11),
что оценки
,
полученные предлагае
-
мым в настоящей работе методом
,
точнее в
2–50
раз по сравнению с
оценками
,
полученными методом
,
программно обеспеченным в систе
-
ме
Maple 7,
применять который можно в случае линеаризации регрес
-
сионной модели
.
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
4
19


