r
(
X, θ
) = e
X
3
θ
−
2
ch(
θ
−
1
)
,
(7)
где
C
= 10
/
max
ℵ
r
(
·
, θ
)
,
ℵ
= (
a, b
)
.
Область
ℵ
зависела от значения
θ
и
задавалась таким образом
,
чтобы функция регрессии проявляла или не
проявляла существенную нелинейность
.
В достаточно узком интервале
(
a, b
)
функция регрессии становится гладкой
.
Моделирование погреш
-
ностей
δ
и
ε
предиктора и отклика осуществлялось программой
random
статистического пакета
Stats
системы
Maple.
Погрешности
δ
и
ε
строились как выборки объема
n
композиций
двух случайных величин
:
δ
=
δ
1
+
δ
2
,
ε
=
ε
1
+
ε
2
.
Составляющие
δ
1
и
ε
1
генерировались по законам нормального распределения с начальными
моментами
Eε
1
= 0
,
Eδ
1
= 0
,
Eε
2
1
=
σ
2
1
,
Eδ
2
1
=
σ
2
2
,
где
σ
1
=
max
ℵ
r
(
·
, θ
)
−
min
ℵ
r
(
·
, θ
)
20
, σ
2
=
b
−
a
20
k
, k
= 1
,
2
.
Составляющие
δ
2
и
ε
2
генерировались либо равномерно распреде
-
ленными случайными величинами на интервале
(0
, σ
1
)
для
ε
2
и на ин
-
тервале
(0
, σ
2
/k
)
,
k
= 1
,
2
,
для
δ
2
,
либо как случайные величины по
-
казательного распределения с параметрами
2
/σ
1
для
ε
2
и
3
/σ
2
для
δ
2
.
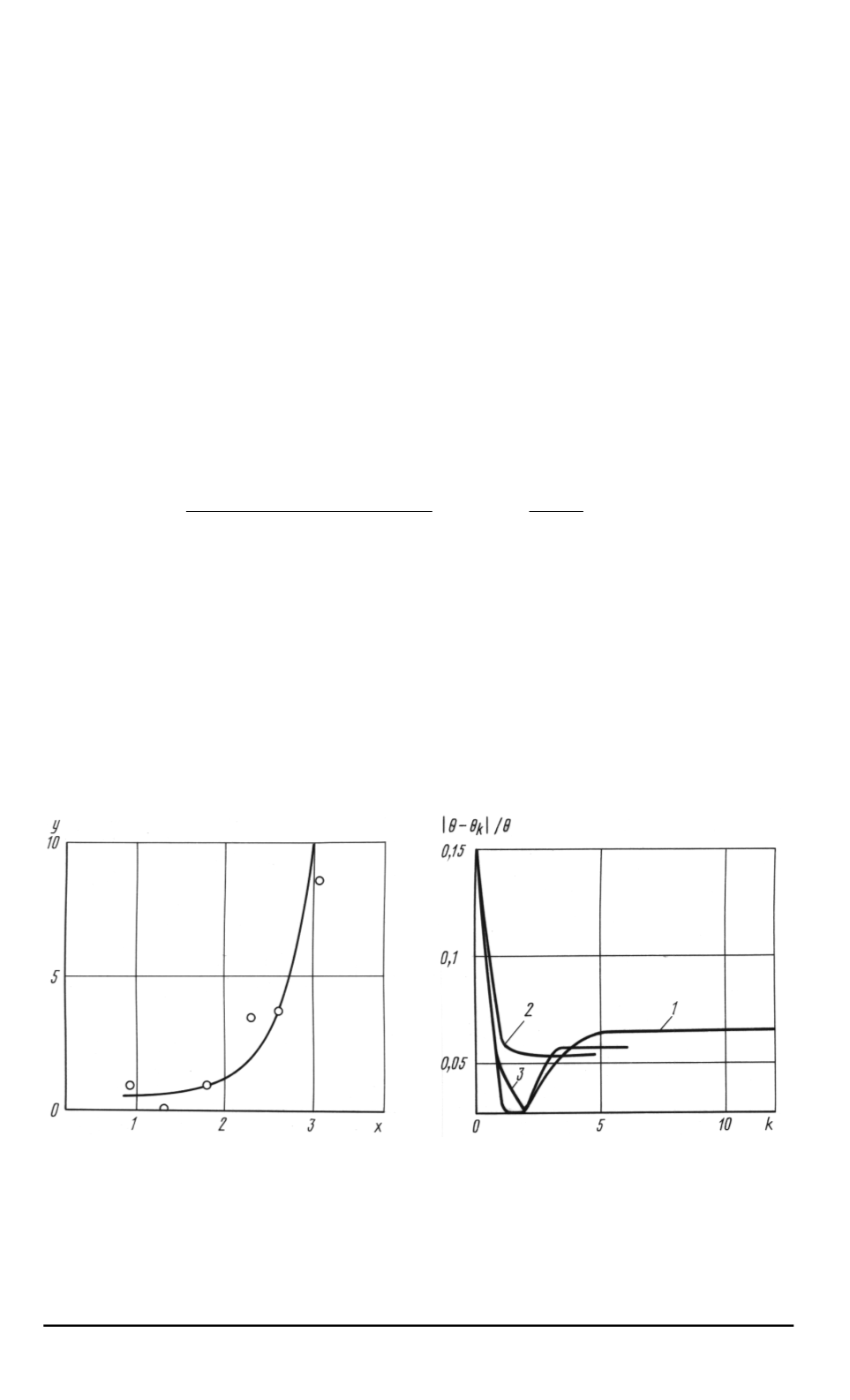
Один из результатов такого моделирования представлен на рис
. 2.
На рис
. 3
приведены зависимости значений относительной погреш
-
ности
|
θ
−
θ
k
|
/θ
оцениваемого параметра от номера итерации
k
.
Здесь
Рис
. 2.
Модель регрессионной зависи
-
мости
Y
=
r
(
X, θ
)
вида
(6);
◦
—
точки
с координатами
(
x
i
, y
i
)
,
x
i
=
X
i
+
δ
i
,
y
i
=
r
(
X
i
, θ
) +
ε
i
Рис
. 3.
Зависимость относительной
погрешности
|
θ
−
θ
k
|
/θ
оценки па
-
раметра
θ
от номера итерации
k
до
изменения условия конца итерации
для случаев использования весовых
функций МО
(
1
),
ОНК
(
2
),
СОМ
(
3
)
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
4
17


