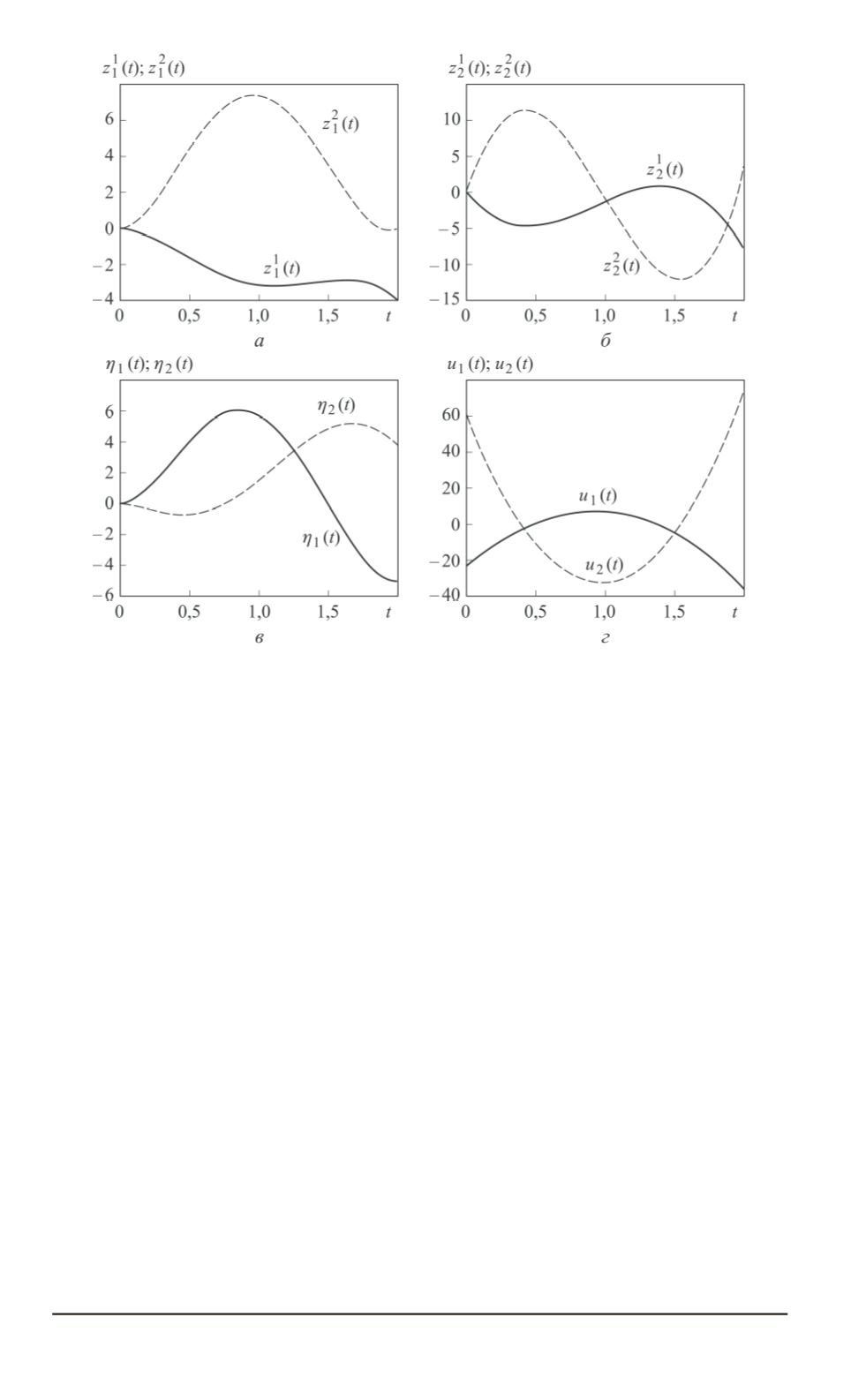
Функции
z
1
1
(
t
)
,
z
2
1
(
t
)
(
а
),
z
1
2
(
t
)
,
z
2
2
(
t
)
(
б
),
η
1
(
t
)
,
η
2
(
t
)
(
в
) и
u
1
(
t
)
,
u
2
(
t
)
(
г
)
Заключение.
Рассмотрена терминальная задача для аффинных си-
стем, не линеаризуемых обратной связью. Предполагалось, что глад-
кой невырожденной заменой переменных в пространстве состояний
система может быть преобразована к регулярному квазиканоническо-
му виду. При этом терминальная задача для исходной системы пе-
реходит в эквивалентную терминальную задачу для системы квази-
канонического вида. Для системы квазиканонического вида доказано
достаточное условие существования решения терминальной задачи.
На его основе предложен метод решения терминальных задач. Приве-
ден пример построения решения терминальной задачи предложенным
методом для системы шестого порядка.
Работа выполнена при поддержке РФФИ (гранты 14-07-00813,
13-07-00736).
ЛИТЕРАТУРА
1.
Краснощеченко В.И.
,
Крищенко А.П.
Нелинейные системы: геометрические ме-
тоды анализа и синтеза. М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. 520 c.
2.
Елкин В.И.
Редукция нелинейных управляемых систем: дифференциально-
геометрический подход. М.: Наука, 1997. 320 c.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5
29


