
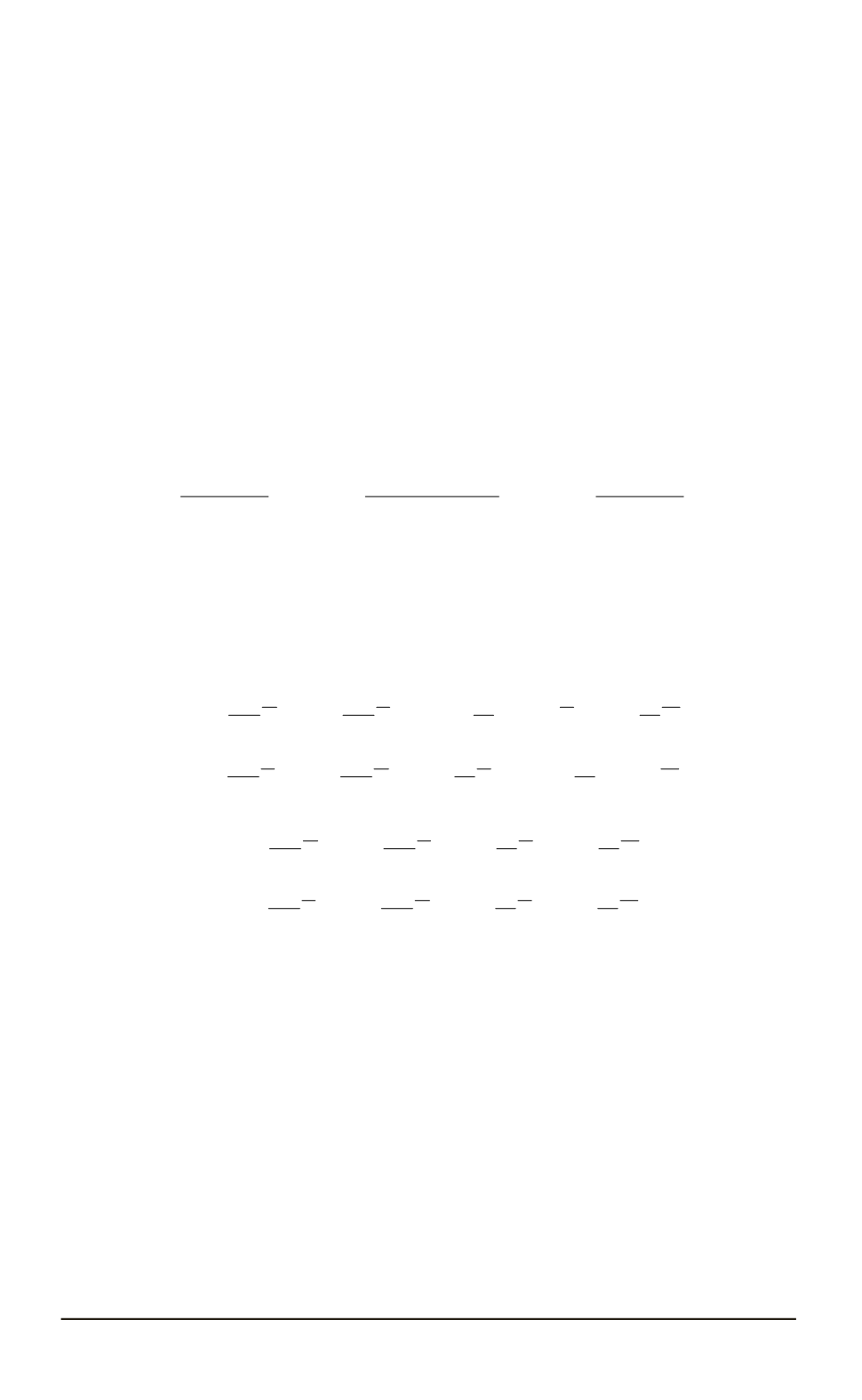
σ
(
j
)
z
(
r, z
) =
−
2
∞
Z
0
h
θ
(
j
)
1
B
j
−
(
−
1)
j
θ
(
j
)
2
C
j
i
s
2
e
sz
J
0
(
sz
)
ds
−
−
2
∞
Z
0
h
(
−
1)
j
θ
(
j
)
3
B
j
+ (
−
1)
j
C
j
sz
i
s
2
e
sz
J
0
(
sz
)
ds
;
(5)
τ
(
j
)
rz
(
r, z
) = 2
∞
Z
0
h
(
−
1)
j
θ
(
j
)
2
B
j
−
θ
(
j
)
1
C
j
i
s
2
e
sz
J
1
(
sz
)
ds
+
+ 2
∞
Z
0
h
θ
(
j
)
3
B
j
+ (
−
1)
j
C
j
sz
i
s
2
e
sz
J
1
(
sz
)
ds,
(6)
где
θ
(
j
)
1
=
μ
2
j
λ
j
+ 3
μ
j
;
θ
(
j
)
2
=
(
λ
j
+ 2
μ
j
)
μ
j
λ
j
+ 3
μ
j
;
θ
(
j
)
3
=
λ
j
+
μ
j
λ
j
+ 3
μ
j
,
j
= 1
,
2;
J
k
(
x
)
,
k
= 0
,
1
— функции Бесселя;
B
j
, C
j
,
j
= 1
,
2
— неизвестные
постоянные, подлежащие определению.
Использовав формулы (3)–(6), выполним условия вспомогательной
задачи и выразим неизвестные постоянные
B
j
, C
j
через функции (2).
Получим
B
1
(
s
) =
d
0
s
Δ
σ
(
s
)
−
d
1
s
Δ
τ
(
s
)
−
b
0
Δ
−
1
u
(
s
)
−
b
1
Δ
w
(
s
) ;
C
1
(
s
) =
d
0
s
Δ
τ
(
s
)
−
d
1
s
Δ
σ
(
s
)
−
b
1
Δ
u
(
s
)
−
b
0
Δ
−
1
w
(
s
) ;
B
2
(
s
) =
d
0
s
Δ
σ
(
s
)
−
d
1
s
Δ
τ
(
s
)
−
b
0
Δ
u
(
s
)
−
b
1
Δ
w
(
s
) ;
C
2
(
s
) =
d
0
s
Δ
τ
(
s
)
−
d
1
s
Δ
σ
(
s
)
−
b
1
Δ
u
(
s
)
−
b
0
Δ
w
(
s
)
.
Здесь
b
0
=
θ
(1)
2
θ
(1)
2
+
θ
(2)
2
−
θ
(1)
1
θ
(1))
1
−
θ
(2)
1
;
b
1
=
θ
(1))
1
θ
(1)
2
+
θ
(2)
2
−
θ
(1))
2
θ
(1))
1
+
θ
(2))
1
;
b
2
= 2
θ
(1)
1
Δ +
θ
(1)
1
b
0
+
θ
(1)
2
b
1
;
b
3
= 2
θ
(1)
2
Δ +
θ
(1)
1
b
1
+
θ
(1)
2
b
0
;
d
0
=
θ
(1)
1
−
θ
(2)
1
.
2;
b
1
=
θ
(1)
2
+
θ
(2)
2
.
2;
Δ =
θ
(1)
1
−
θ
(2)
1
2
−
θ
(1)
2
+
θ
(2)
2
2
;
34
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3

















