
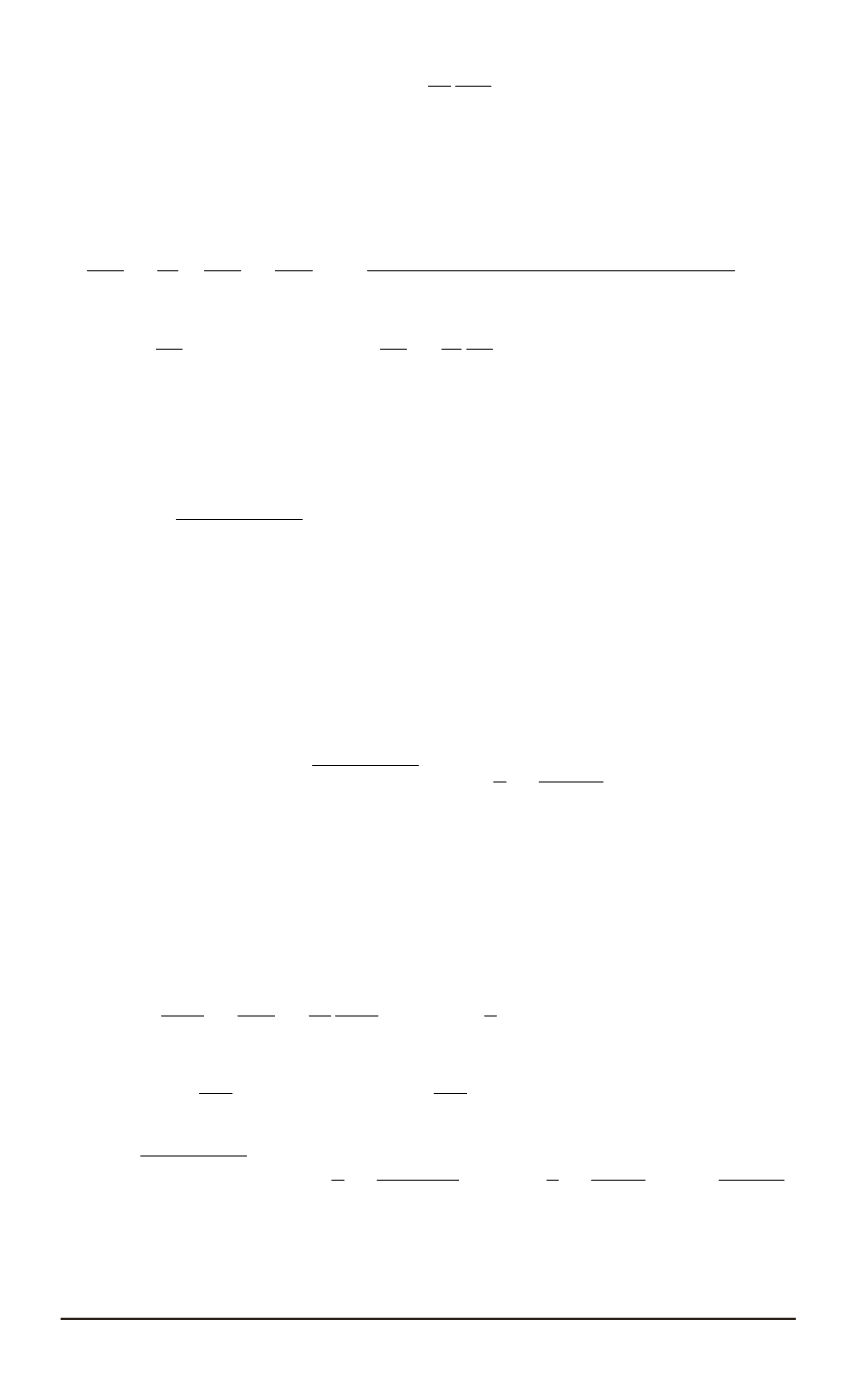
где
c
2
=
ω
2
/
(
N
2
−
ω
2
)
;
N
2
(
z
) =
−
g
ρ
0
∂ρ
0
∂z
— частота Брента – Вяйсяля,
которая предполагается постоянной,
N
(
z
) =
N
=
const. В приближе-
нии Буссинеска система (3) сводится к одному уравнению, например,
для возмущенного давления
p
с соответствующими граничными усло-
виями
∂
2
p
∂z
2
−
1
c
2
∂
2
p
∂y
2
+
∂
2
p
∂x
2
=
−
iωQρ
0
δ
(
x
−
x
0
)
δ
(
y
−
y
0
)
δ
(
z
−
z
0
)
c
2
;
(4)
∂p
∂z
= 0
при
z
= 0
,
∂p
∂z
−
γ
c
2
∂p
∂y
= 0
при
z
=
−
γy.
(5)
Под значением
ρ
0
в правой части условия (4) в силу относитель-
но малого изменения плотности
ρ
0
(
z
)
в океане понимается, на-
пример, значение плотности морской воды на поверхности, т.е.
ρ
0
=
ρ
0
(0) =
const. Решение
p
(
x, y, z
)
должно стремиться к ну-
лю при
p
x
2
+
y
2
+
z
2
→ ∞
. После нахождения функции
p
(
x, y, z
)
компоненты скорости
(
U
1
, U
2
, W
)
можно определить из первых трех
уравнений системы (3), а плотность
ρ
— из пятого уравнения этой
системы.
Интегральные представления решений.
Выполним замену пе-
ременных
y
=
r
ch
ϕ, z
=
−
cr
sh
ϕ
;
r
=
p
y
2
−
z
2
/c
2
;
ϕ
=
1
2
ln
cy
−
z
cy
+
z
.
(6)
Осуществим преобразование Фурье по переменной
x
(не умаляя
общности можно принять
x
0
= 0
). Учитывая, что модуль якобиана
перехода от координат
(
y, z
)
к координатам
(
r, ϕ
)
равен
cr
, из (4), (5)
получаем для фурье-образа
P
(
r, ϕ, l
)
функции
p
(
r, ϕ, x
)
следующую
плоскую краевую задачу:
∂
2
P
∂r
2
+
∂P
r∂r
−
1
r
2
∂
2
P
∂ϕ
2
−
l
2
P
=
q
r
δ
(
r
−
r
0
)
δ
(
ϕ
−
ϕ
0
);
(7)
∂P
∂ϕ
= 0
при
ϕ
= 0
,
∂P
∂ϕ
= 0
при
ϕ
=
ϕ
r
;
(8)
r
0
=
q
y
2
0
−
z
2
0
/c
2
, ϕ
0
=
1
2
ln
cy
0
−
z
0
cy
0
+
z
0
, ϕ
r
=
1
2
ln
c
+
γ
c
−
γ
, q
=
iωQρ
0
c
.
(9)
Решение трехмерной краевой задачи (4), (5) в переменных
(
r, ϕ, x
)
получается из решения плоской задачи (7), (8) с помощью обратного
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3
61

















