
найдем
a
1
= 1
, a
2
= 0
, a
3
=
1
12
˙
x
∗
f
, a
5
=
1
40
˙
x
∗
f
1
12
˙
x
∗
f
−
1
,
a
6
=
−
1
2
+
1
6
˙
x
∗
f
a
4
, . . .
(13)
В асимптотическом представлении (13) имеется единственный не-
определенный коэффициент
a
4
, каждому значению которого соответ-
ствует некоторый конкретный вид формы поверхности жидкой пленки
вблизи линии трехфазного контакта, т.е. при фиксированном значении
скорости
˙
x
∗
f
асимптотическое представление (13) определяет однопа-
раметрическое семейство интегральных кривых для уравнения (8) с
граничными условиями (10). Указанное асимптотическое представле-
ние для заданной скорости
˙
x
∗
f
<
0
и произвольно задаваемого ко-
эффициента
a
4
использовалось для вычисления начального значения
толщины жидкой пленки и всех необходимых производных при чи-
сленном интегрировании уравнения (8).
Общие физические соображения о характере поведения интеграль-
ной кривой при больших значениях толщин жидкой пленки требуют
ограничения на знак коэффициента
a
4
<
0
. Лишь при этом условии
кривизна свободной поверхности жидкости оказывается в среднем по
модулю убывающей по толщине свободной поверхности функцией.
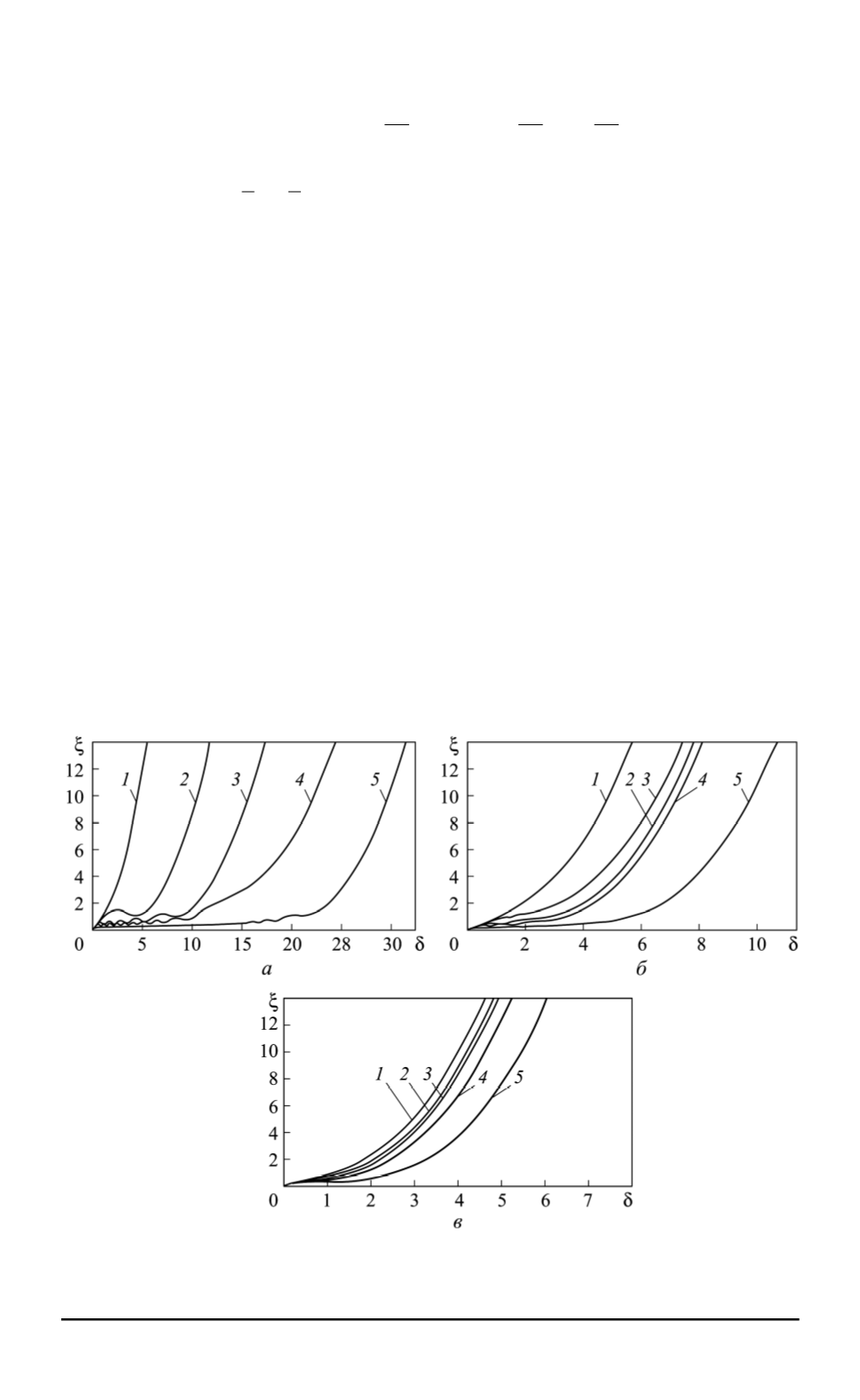
Рис. 2. Профили решений при
˙
x
∗
f
=
−
0
,
5
∗
f
∗
f
(
а
), – 2,0 (
б
) и – 5,0 (
в
) для значений
постоянной
a
4
= 0
,
1
(
1
), – 0,05 (
2
), – 0,5 (
3
), – 1,0 (
4
) и – 5,0 (
5
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 5
95
















