
38
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». 2016. № 3
2
= ,
x y
3
=
/ ( );
x I mg r
тогда стабилизируемое положение равно-
весия исходной системы будет соответствовать нулевому положению
равновесия системы в новых переменных
1 2
2
1
2
3
3
3
;
(
)
;
( )
1 .
( )
x x
x r
mg
x g
x
m
r
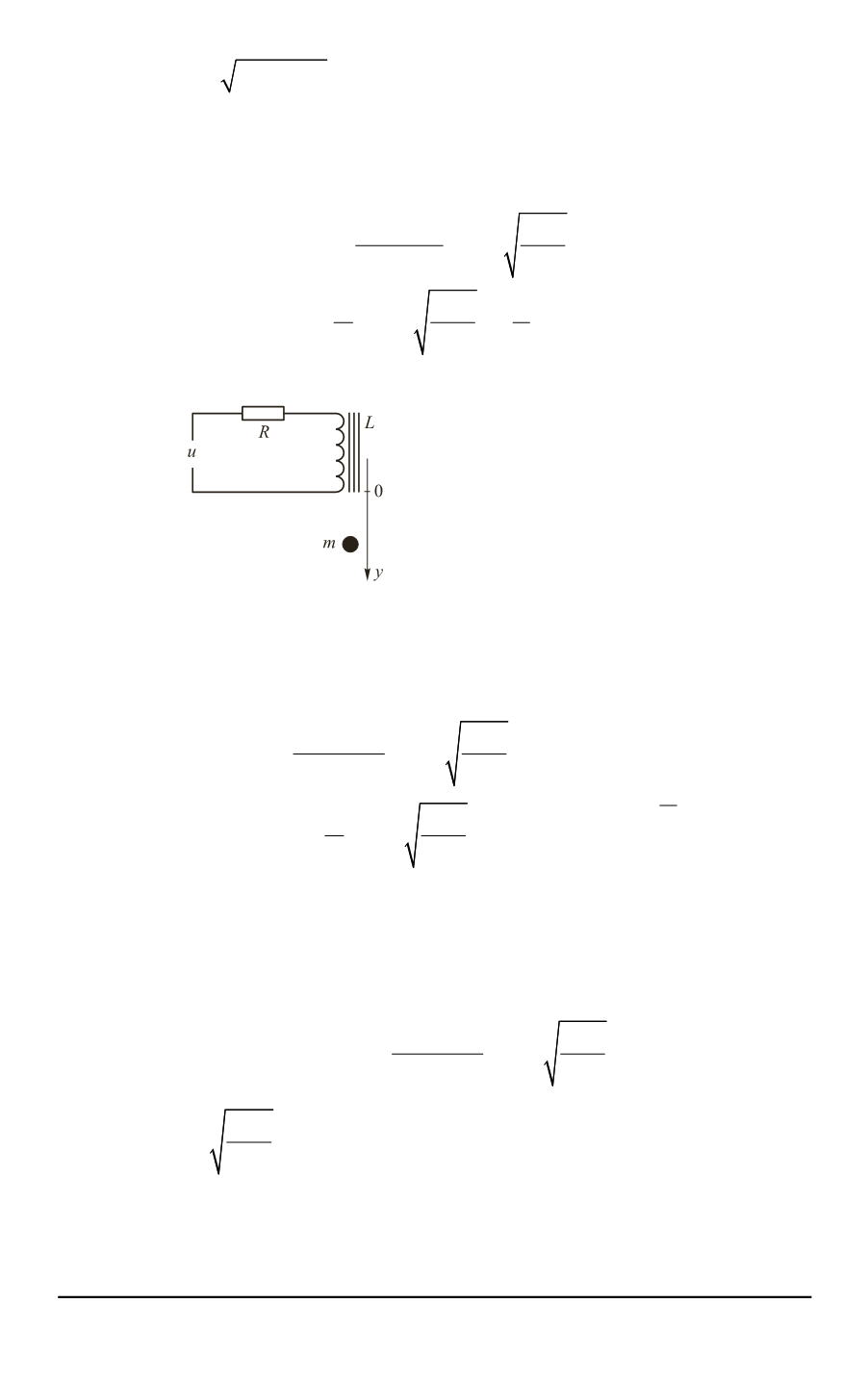
R
mg
x
x
u
L
r
L
(24)
Получим эквивалентную систему канонического вида для системы
без возмущений (24)
2
2
1
3
3
0
( ) =
,
( ) = 0 ;
( )
1
( )
x
x r
mg
A x g
x
B x
m
r
R
mg
L
x
L
r
решая систему в частных производных
= 0,
B
[ , ] = 0,
A B
находим
1
( ) = ,
x x
отсюда
1
1 2
2
2
1
2
3
3
= = ,
= = ,
= =
.
( )
z
x z A x
x r
mg
z A g
x
m
r
(25)
Если
3
( )
mg
x
r
, т. е. ток
,
I
сохраняет свой знак, то система (25)
является гладкой невырожденной заменой переменных. Для опре-
деленности в окрестности положения равновесия будем полагать ток
I
положительным. Тогда за область определения диффеоморфизма
Рис. 2.
Обобщенная модель
левитации под воздействием
электромагнита
















