
Сравнительный анализ оценок теплопроводности…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 5
75
ние значений
и
,
а при
=1000
различием кривых
и
можно прене-
бречь. Таким образом, и оценки, определяемые по соотношению (17), не обес-
печивают заметное снижение возможной погрешности при большом отклоне-
нии значения
от единицы. Полученные двусторонние оценки не учитывают
конкретное расположение волокон в композите. Вариационный подход, осно-
ванный на двойственной вариационной формулировке задачи установившейся
теплопроводности, позволяет при построении оценок использовать информа-
цию о взаимном расположении волокон.
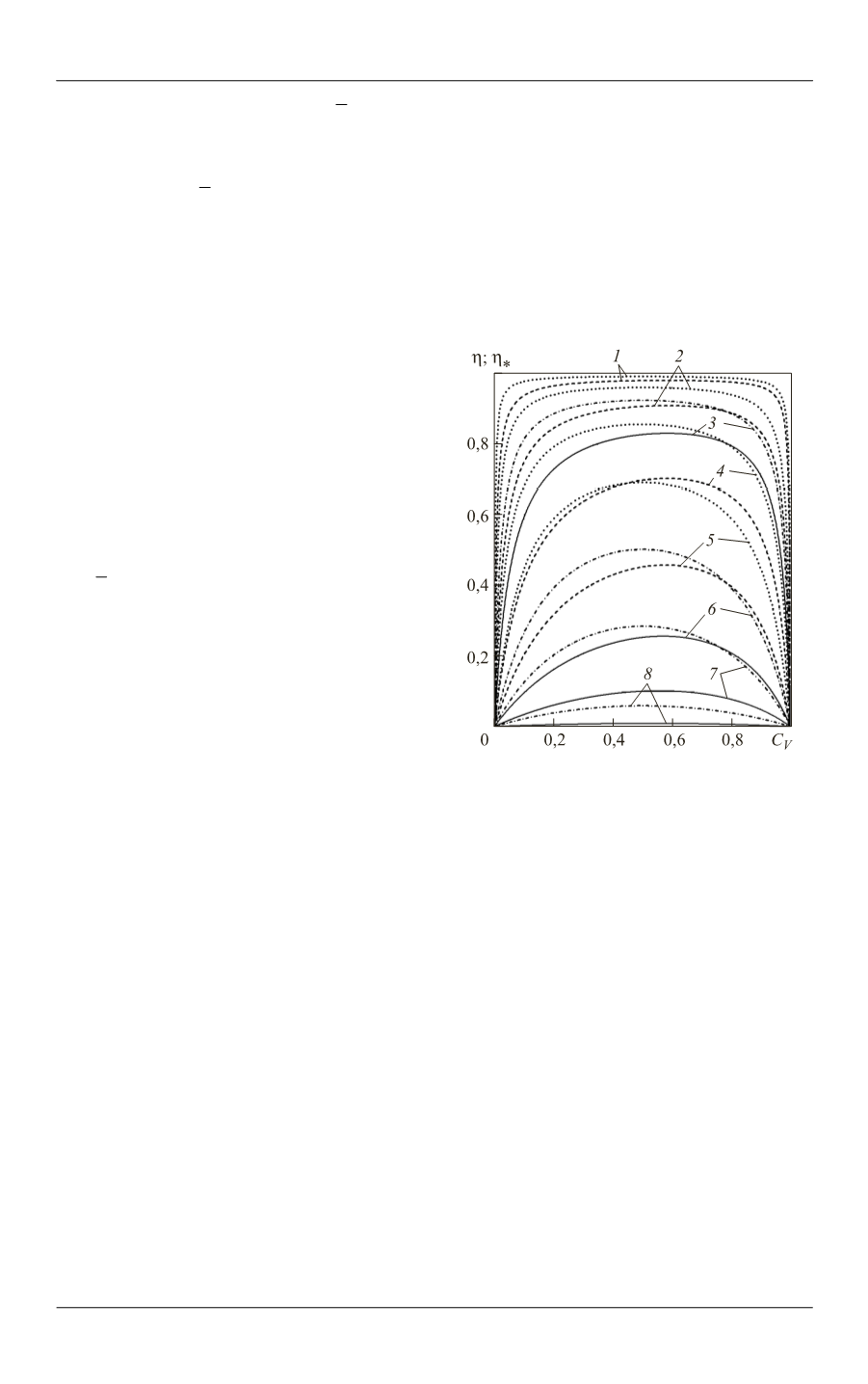
Рис. 1.
Зависимости наибольшей воз-
можной относительной погрешности
вычисления главных значений тензора
эффективной теплопроводности ком-
позита от объемной концентрации
волокон при значениях параметра
= 1000 (
1
), 200 (
2
), 100 (
3
), 50 (
4
),
20 (
5
), 10 (
6
), 5 (
7
) и 2 (
8
):
— пунктирные и штрихпунктирные ли-
нии;
— штриховые и сплошные линии
Влияние взаимного расположения волокон.
Однонаправленный волокни-
стый композит является трансверсально изотропным по отношению к тепло-
проводности не только при хаотическом расположении поперечных сечений
волокон в плоскости рассмотренного выше прямоугольника. Это свойство бу-
дет сохранено, когда центры круговых поперечных сечений волокон одинаково-
го радиуса
r
совпадают с узлами плоской сетки с одинаковыми ячейками в виде
правильных треугольников, квадратов и правильных шестиугольников, по-
скольку ось, проходящая через центр таких многоугольников перпендикулярно
их плоскости, имеет порядок выше второго [17]. Если сетка состоит из одинако-
вых прямоугольных ячеек, то
*
*
2 1
и композит будет ортотропным по отно-
шению к теплопроводности.
Рассмотрим расположение волокон, соответствующее прямоугольной ячейке
со сторонами, равными
1
2
b
и
2
2 .
b
Для определенности примем
1 2
b b
и поме-
стим центр поперечного сечения волокна в одной из вершин прямоугольной
ячейки, совместив с этой вершиной начало локальной прямоугольной декарто-
вой системы координат
1 2
.
O
Выделим в ячейке четвертую часть, содержащую
четверть поперечного сечения волокна радиусом
r
(рис. 2). Остальная площадь
ячейки соответствует матрице композита. При касании соседних волокон
















