
А.В. Хохлов
112
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
ее сдвиг
2
1
(
),
t t
ε = σ Π −
участвующие в двусторонней оценке (24) для КП (23)
(в случае
( )
x x
Φ =
), штриховая линия розового цвета — КП
2
( )
t
ε = σ Π
с
2
σ =
0,5.
Поскольку
(0) 0,
Π =
то в точке
1
t t
=
все КП не имеют разрыва; из
(0)
Π = +∞
сле-
дует, что у всех КП
1
( 0)
t
Π + = ±∞
(знак совпадает с
2 1
sgn(
)).
σ − σ
При любом
2
1
(0; )
σ ∈ σ
у КП есть точка минимума
1
,
m
t t
>
она двигается вправо от
1
t
до
∞
с
убыванием
2
σ
от
1
σ
до нуля: функция
2
( )
m
t
σ
убывает,
(0 ) ,
m
t
+ = ∞
1
1
( 0)
m
t
t
σ − =
[47] (наличие точек экстремума деформации между точками разрыва программы
нагружения наблюдается в испытаниях разных материалов [2, 4, 52–54], но, как
правило, считается признаком нелинейности их поведения
)
. Для любого
1,
u
<
очевидно,
0,
v
=
и потому
2
1
( ( ) (
)) 0
t
t t
σ Π −Π − →
и
2
( )
( ) 0
t
t
ε − σ Π →
при
t
→∞
(точнее,
1
2
2
1 2
1
( )
( ) (
)[
( )]).
u
u
t
t
uat t
O t
−
−
ε − σ Π = σ − σ
+
Таким образом, ширина поло-
сы между штриховыми КП красного цвета стремится к нулю, и эта линейная мо-
дель (класса НеМ) обладает свойством затухания памяти.
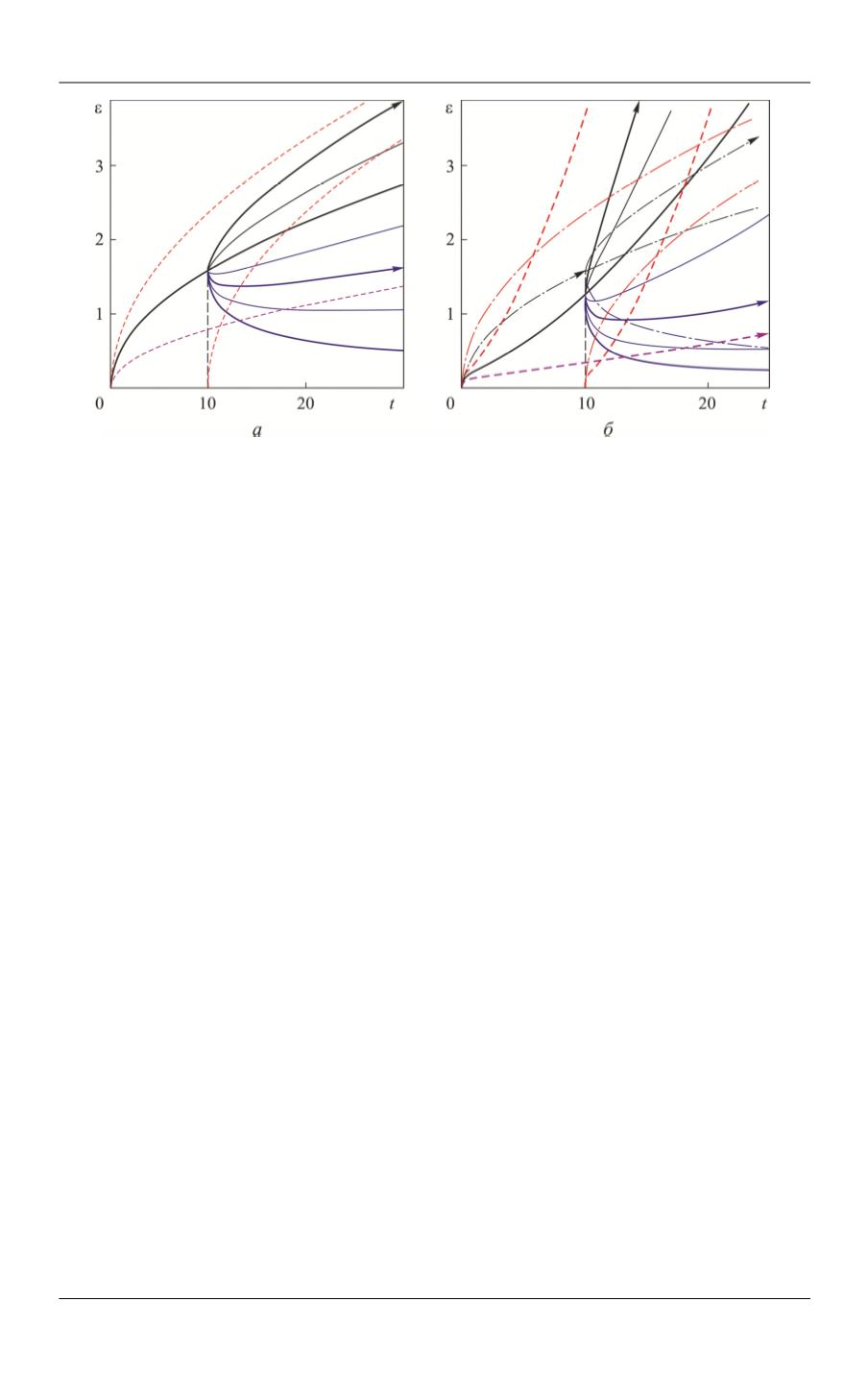
Кривые ползучести (23) (с
σ =
1
1
,
=
1
10
t
и разными
σ
2
) нелинейной модели,
полученной из степенной ФП
Π =
( )
u
t at
с
=
0, 5,
a
=
0, 5
u
введением МФ
Φ
( )
x
вида (21) с
=
3,
m
ϑ =
0, 5,
=
0, 5,
A
приведены на рис. 4,
б
. Параметры программ
нагружения те же:
σ =
1
1,
=
1
10,
t
σ =
2
1; 2,25; 1,5 (КП черного цвета для
σ ≥ σ
2 1
)
и
2
σ =
0,75; 0,5; 0,25; 0 (КП синего цвета для
<
σ σ
2 1
). Поскольку
Π =
(0) 0,
то в точке
=
1
t t
все КП (23) непрерывны. При
Π = +∞
(0)
у всех КП
Π + = ±∞
1
( 0)
.
t
При любом
σ ∈ σ
2
1
(0; )
у КП есть точка минимума
>
1
,
m
t t
кото-
рая двигается вправо от
1
t
до
∞
,
с убыванием
σ
2
от
σ
1
до нуля (
σ
2
( )
m
t
убыва-
ет,
+ = ∞
(0 ) ,
m
t
σ − =
1
1
(
0)
m
t
t
). Штриховые линии красного цвета — обычная КП
2
( ( ))
t
ε = Φ σ Π
и ее сдвиг
2
1
( (
))
t t
ε = Φ σ Π −
с
2
σ =
1,5 участвующие в оценке (24).
Штрихпунктирные линии — КП линейной модели, приведенной на рис. 4,
а
для
сравнения: КП черного цвета — для
σ =
2
1
и
σ =
2
0,
1,5 синего цвета — для
Рис. 4.
Кривые ползучести (23) линейной модели с МФ
u
at
Π =
и
( )
x x
Φ =
(
а
) и нелиней-
ной модели с
u
at
Π =
и
1/
[
(1 ) ]
m
m
A x
x
Φ = ϑ + − ϑ
(
б
) для различных значений
2 1
/
σ σ
















