
Анализ общих свойств кривых ползучести при ступенчатых нагружениях…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
113
σ =
2
0,
т. е. кривая обратной ползучести, красного — вилка оценки (24) для
КП (23) с
σ =
2
1, 5. Хотя у рассматриваемой модели
=
0,
v
линейная модель с ФП
Π =
( )
u
t at
обладает свойством затухания памяти, введение МФ
Φ
( )
x
вида (21)
меняет ситуацию: при заданных значениях
=
0, 5,
u
=
3
m
не выполняется дока-
занный выше критерий затухания памяти (22) для моделей семейства (21). Их КП
(23) не сходятся к обычной КП и отклонение
Δ
( )
t
стремится к бесконечности при
→∞
.
t
Соответственно, полоса между штриховыми линями красного цвета, при-
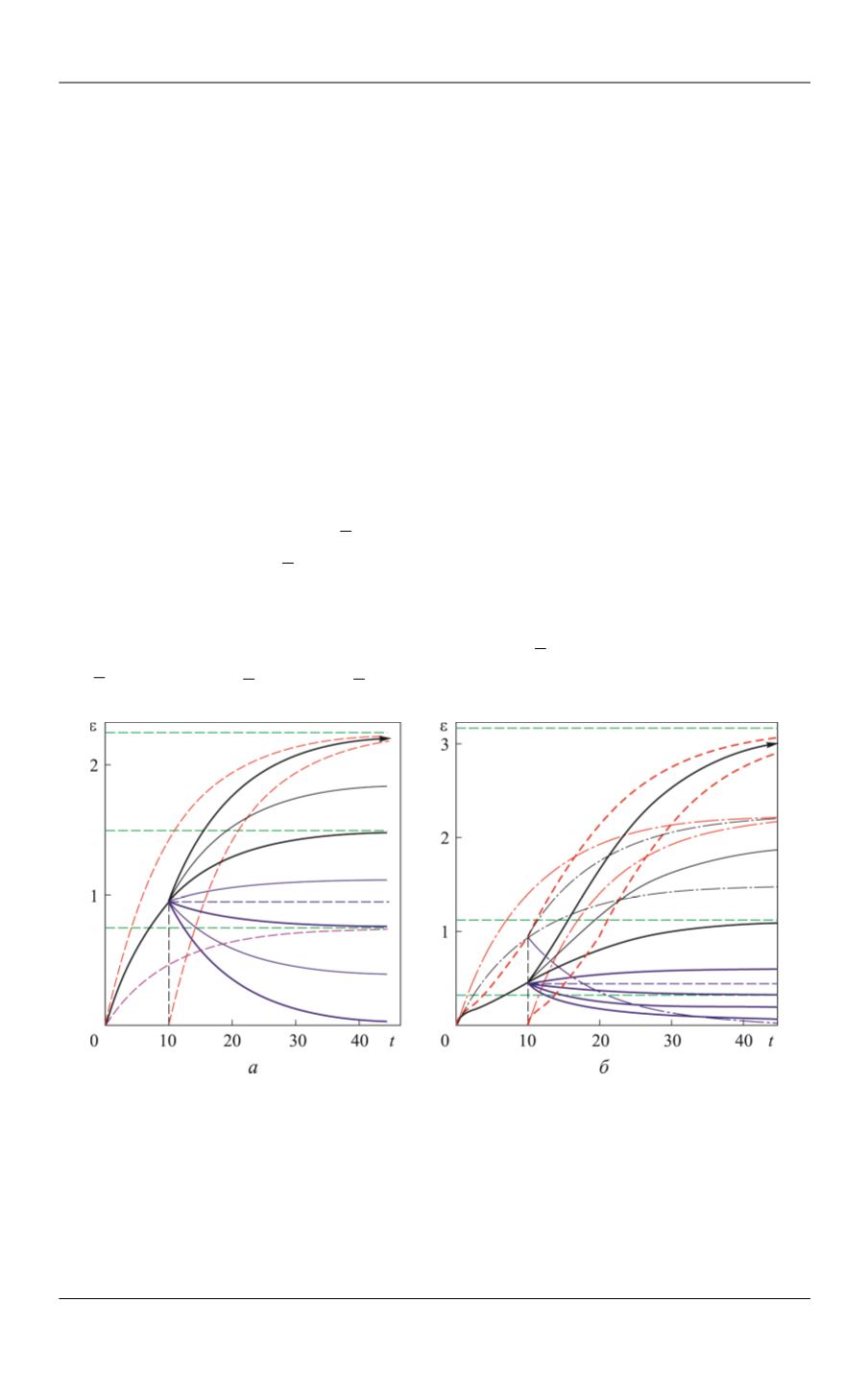
веденными на рис. 4,
б
, не стягивается до нуля, а неограниченно расширяется.
Кривые ползучести (23) (сингулярной) линейной
модели Фойгта
−λ
Π = β −β
(
e ,
t
λ =
0,1,
γ =β =
1, 5
) для
=
1
10,
t
σ =
1
1
и тех же значений
σ
2
при-
ведены на рис. 5,
а
. Каждая КП имеет горизонтальную асимптоту
ε = σ β
2
(пря-
мые зеленого цвета). Поскольку
=
0,
v
то эта модель обладает свойством затуха-
ния памяти (полоса между штриховыми линиями красного цвета, изображаю-
щими вилку двусторонней оценки (24) для КП с
2
σ =
1,5 стягивается до нуля).
Особенность КП модели Фойгта (и КП РеМ-3) — отсутствие точки минимума на
всех КП с
2 1
:
σ < σ
при
2
2
1
1
:
(1 exp(
))
t
σ > σ = σ − −λ
КП (23) возрастает на всем
луче
1
,
t t
≥
а при
2 2
σ < σ
КП (23) убывает [47]. Таким образом, для РеМ-3 и
СиМ-2 смена возрастания КП на убывание (а также выпуклости) происходит
тотально
на всем луче
1
,
t t
≥
синфазно во всех точках
. Штриховая линия сине-
го цвета, приведенная на рис. 5,
а
, — КП при
2 2
σ = σ
(для
0,1
λ =
и
1
10
t
=
име-
ем
2
1
0, 63 ,
σ ≈ σ
2
2
( ,
) ( )
t
ε σ ≡ ε ∞ = σ β
).
Рис. 5.
Кривые ползучести (23) линейной модели Фойгта
(
e ,
t
−λ
Π = β − β
( ) )
x x
Φ =
(
а
) и
нелинейной модели с
e
t
−λ
Π = β − β
и
1/
[
(1 ) ]
m
m
A x
x
Φ = ϑ + − ϑ
(
б
) для различных значений
2 1
/
σ σ
Кривые ползучести (23) нелинейной модели, полученной из модели Фойгта
введением (той же) МФ
( )
x
Φ
вида (21) с
3,
m
=
0, 5,
ϑ=
0, 5,
A
=
приведены на
рис. 5,
б
. Параметры программ нагружения те же:
1
1;
σ =
1
10;
t
=
2
1; 1, 25; 1, 5
σ =
















