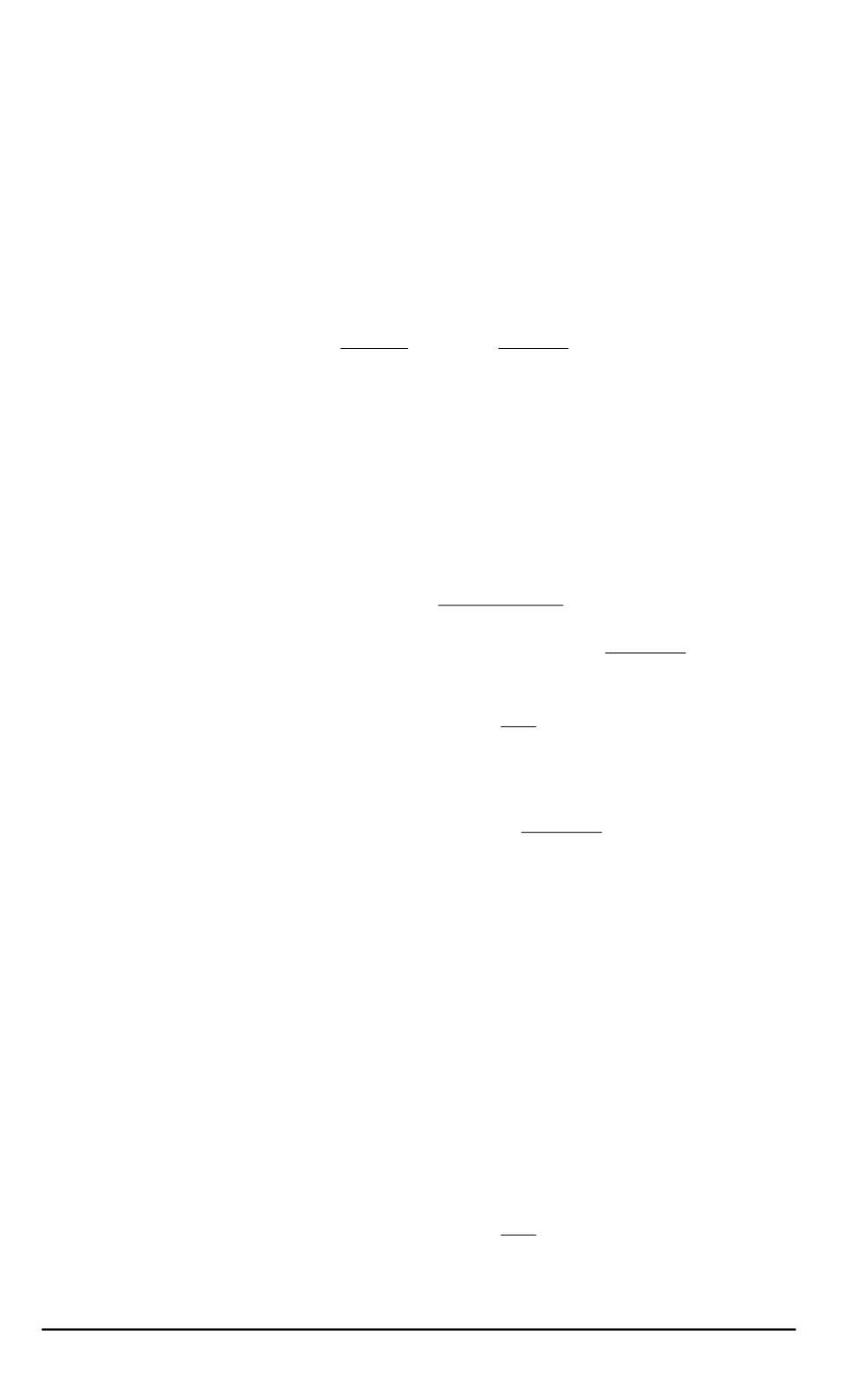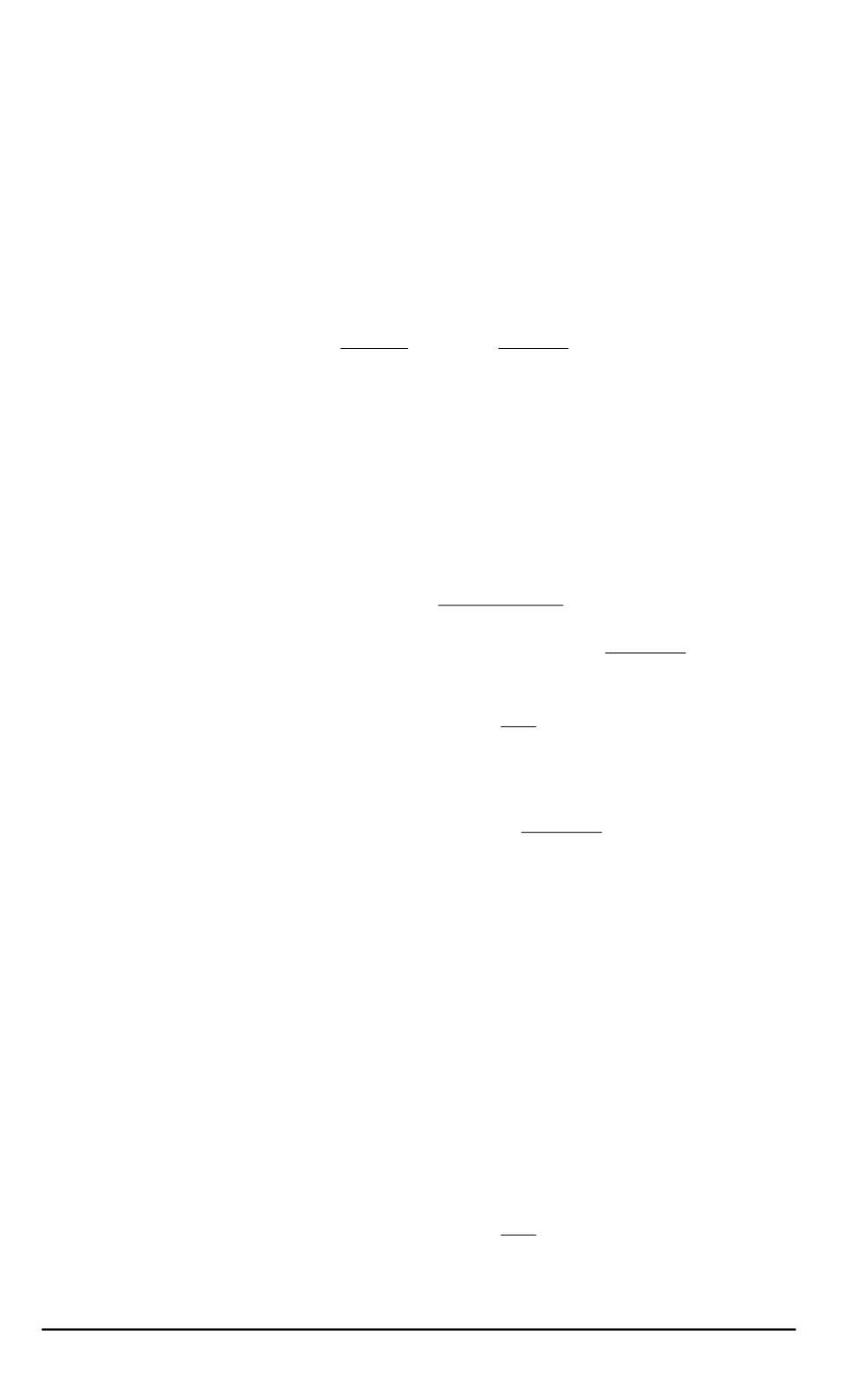
который будем называть специальным квазиканоническим видом. Та-
кой вид более удобен для анализа свойств системы.
Условия существования квазиканонического вида.
Следуя ра-
ботам [5, 6], приведем результаты, относящиеся к преобразованию
аффинных систем (1) к квазиканоническому виду (2).
Напомним, что коммутатором гладких векторных полей
X
и
Y
называют [11] векторное поле
[
X, Y
]
, координаты которого можно вы-
числить через координаты
X
(
x
)
и
Y
(
x
)
векторных полей
X
и
Y
по
формуле
[
X, Y
](
x
) =
∂Y
(
x
)
∂x
X
(
x
)
−
∂X
(
x
)
∂x
Y
(
x
)
.
Зададим последовательность коммутаторов векторных полей
A
и
B
:
ad
0
A
B
=
B
,
ad
1
A
B
= [
A, B
]
,
ad
k
+1
A
B
= [
A,
ad
k
A
B
]
,
k
≥
1
.
Теорема 1.
[5]
Для того чтобы в некоторой области
Ω
для аф-
финной системы
(1)
существовали переменные, в которых она име-
ет квазиканонический вид
(2)
, необходимо и достаточно, чтобы су-
ществовала функция
ϕ
(
x
)
2
C
∞
(Ω)
,
удовлетворяющая в
Ω
системе
уравнений
ad
k
A
Bϕ
(
x
) = 0
, k
= 0
, r
−
2
,
(7)
и существовали функции
η
j
=
η
j
(
x
)
2
C
∞
(Ω)
, j
= 1
, n
−
r,
которые
вместе с функциями
z
i
=
A
i
−
1
ϕ
(
x
)
, i
= 1
, r,
(8)
задают в
Ω
гладкую невырожденную замену переменных
(
z, η
) =
ϕ
(
x
)
.
Следствие 1.
Пусть выполнены условия теоремы 1 и дополнитель-
ные координатные функции
η
j
=
η
j
(
x
)
,
j
= 1
, n
−
r
, удовлетворяют в
области
Ω
соотношениям (5). Тогда в
Ω
аффинная система (1) заменой
переменных
(
z, η
) =
ϕ
(
x
)
преобразуется к специальному квазикано-
ническому виду (6).
Локальные условия существования квазиканонического вида
.
Локальные условия, при которых аффинная система преобразуется к
квазиканоническому виду, задает следующая теорема.
Теорема 2.
Для того чтобы в некоторой окрестности точки
x
0
для аффинной системы
(1)
существовали переменные
,
в которых она
имеет квазиканонический вид
(2)
, необходимо и достаточно, чтобы
существовала гладкая функция
ϕ
(
x
)
,
удовлетворяющая в окрестно-
сти точки
x
0
системе уравнений
(7)
,
и ранг матрицы Якоби отобра-
жения
z
i
=
A
i
−
1
ϕ
(
x
)
, i
= 1
, r,
(9)
в точке
x
0
был равен
r
.
6
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1