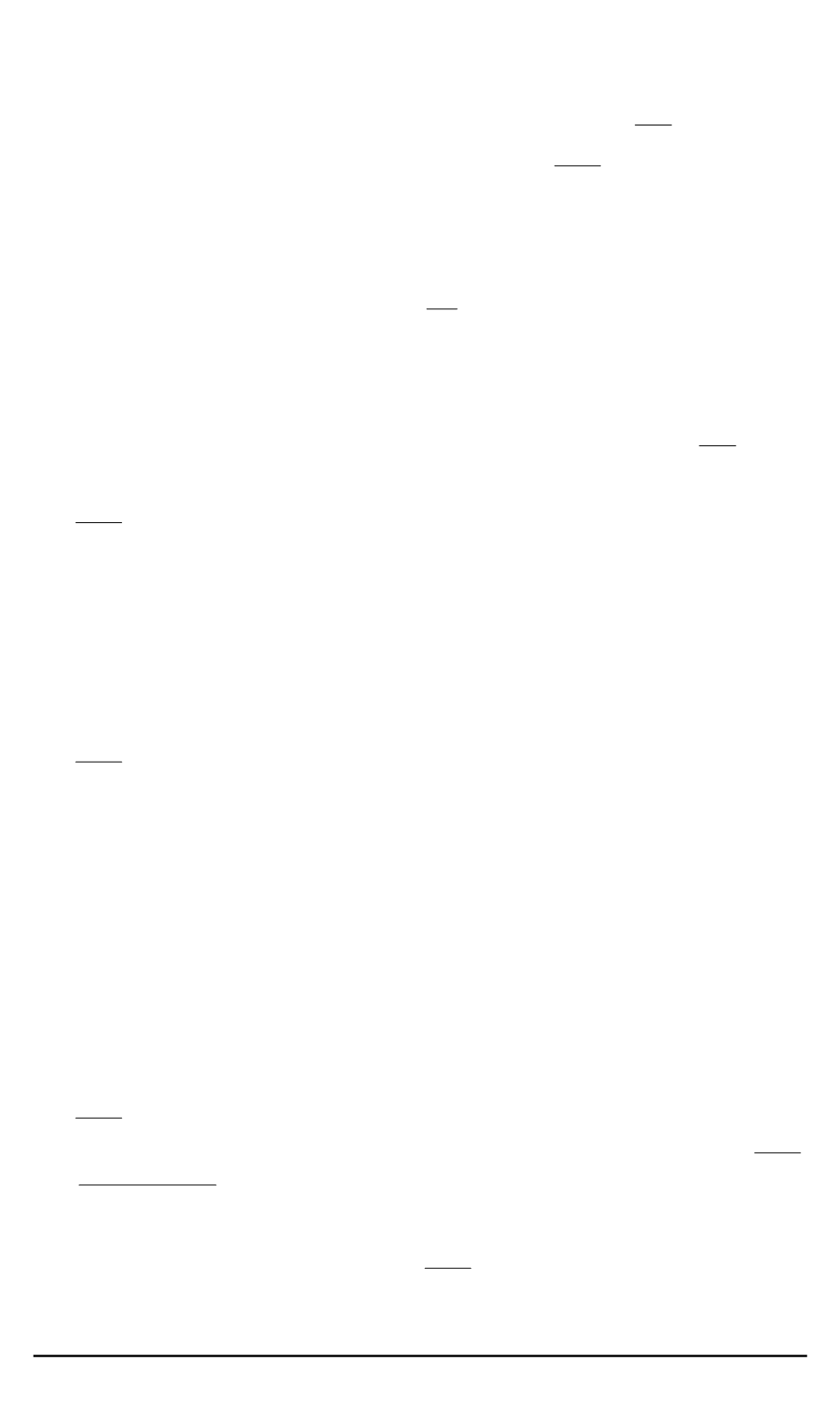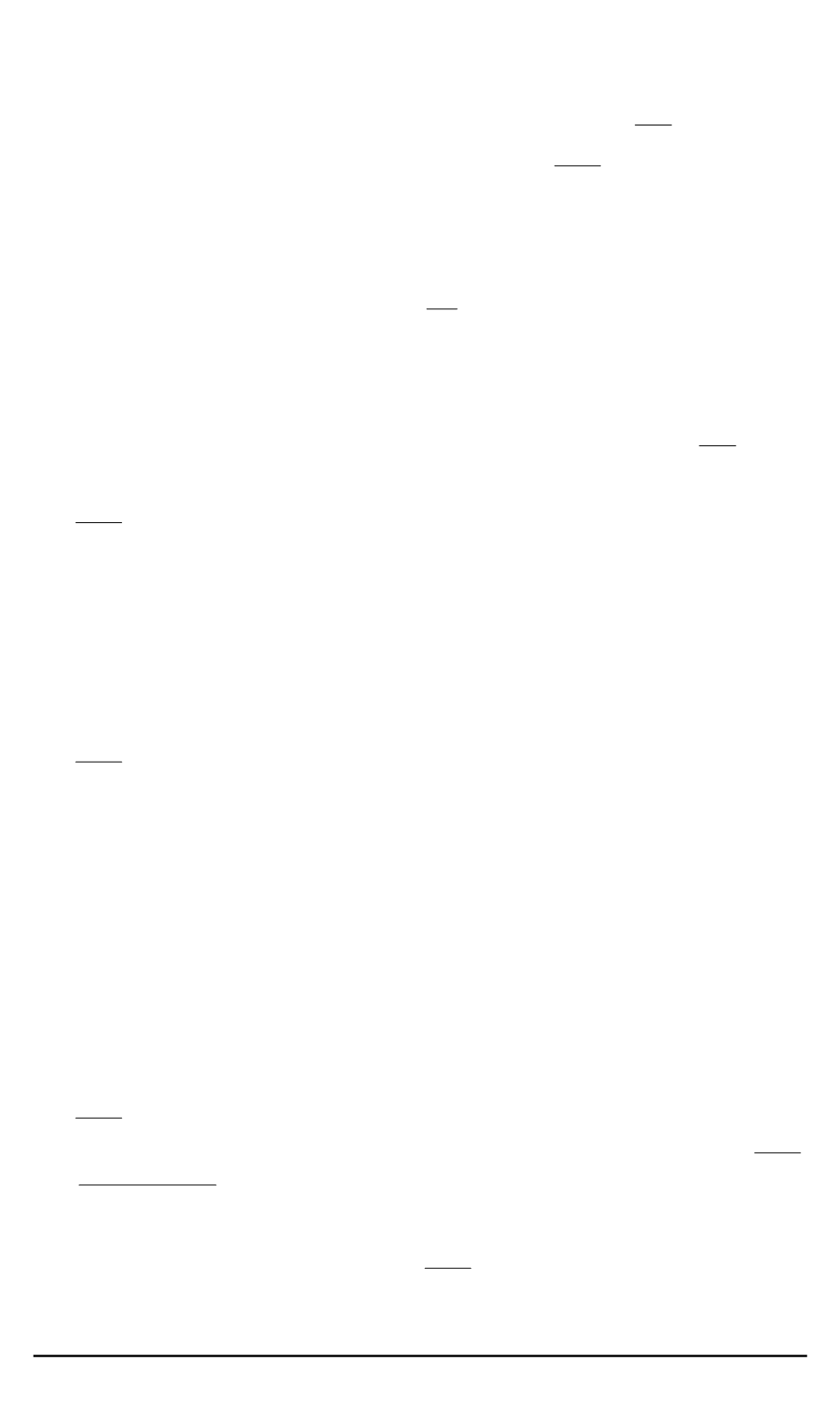
Система (1) преобразуется к виду
y
(
k
i
)
i
=
φ
i
(
t, y
1
, . . . , y
(
k
p
−
1)
p
, z
1
, . . . , z
(
s
m
−
r
m
−
1)
m
,
v
1
, . . . , v
(
r
1
)
1
, v
2
, . . . , v
(
r
m
)
m
)
, i
= 1
, p,
(10)
z
(
s
i
−
r
i
)
i
=
v
i
при
s
i
−
r
i
>
0
, i
= 1
, m.
(11)
Обозначим через
R
старший порядок производной управления в
системе (10):
R
= max
i
=1
,m
r
i
.
(12)
Тогда система (10) примет вид
y
(
k
i
)
i
=
φ
i
(
t, y
1
, . . . , y
(
k
p
−
1)
p
, z
1
, . . . , z
(
s
m
−
r
m
−
1)
m
, v
1
, . . .
. . . , v
(
R
)
1
, v
2
, . . . , v
(
R
)
m
)
, i
= 1
, p,
(13)
где переменные
z
i
и их производные входят в систему при
s
i
−
r
i
>
0
,
i
= 1
, m
.
Модуль
H
1
для отображения вход-выход (13), (14) определяется
как
H
1
= span
F
{
dt, dy
1
, d
˙
y
1
, . . . , dy
(
k
1
−
1)
1
, dy
2
, d
˙
y
2
, . . . , dy
(
k
p
−
1)
p
, dz
1
, . . .
. . . , dz
(
s
1
−
r
1
−
1)
1
, dz
2
, . . . , dz
(
s
m
−
r
m
−
1)
m
, dv
1
, . . . , dv
(
R
−
1)
1
, dv
2
, . . . , dv
(
R
−
1)
m
}
,
где переменные
dz
i
и их производные входят в систему при
s
i
−
r
i
>
0
,
i
= 1
, m
.
Модули
H
i
, i
= 2
,
3
, . . . ,
находят по (7).
Теорема 2.
Реализация вида
(3)
,
(6)
локально существует для урав-
нений
(1)
отображения вход-выход тогда и только тогда
,
когда для
системы уравнений
(13)
,
(14)
модуль
H
R
+1
имеет базис из точных
1
-форм.
J
Необходимость.
Пусть существует реализация вида (3), (6). По-
сле замены (8), (9) система (6) имеет вид
˙
x
=
f
(
t, x, z
1
, . . . , z
(
s
1
−
r
1
−
1)
1
, z
2
, . . . , z
(
s
m
−
r
m
−
1)
m
, v
)
,
(14)
где переменные
z
i
и их производные входят в систему при
s
i
−
r
i
>
0
,
i
= 1
, m
.
Вводим дополнительные переменные
z
ij
при
s
i
−
r
i
>
0
,
i
= 1
, m
,
j
= 0
, s
i
−
r
i
−
1
, и получаем систему
˙
z
i
0
=
z
i
1
, . . . ,
˙
z
i,s
i
−
r
i
−
2
=
z
i,s
i
−
r
i
−
1
,
˙
z
i,s
i
−
r
i
−
1
=
v
i
,
(15)
при
s
i
−
r
i
>
0
, i
= 1
, m
;
˙
x
=
f
(
t, x, z
10
, . . . , z
1
,s
1
−
r
1
−
1
, z
20
, . . . , z
m,s
m
−
r
m
−
1
, v
)
.
(16)
6
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 3