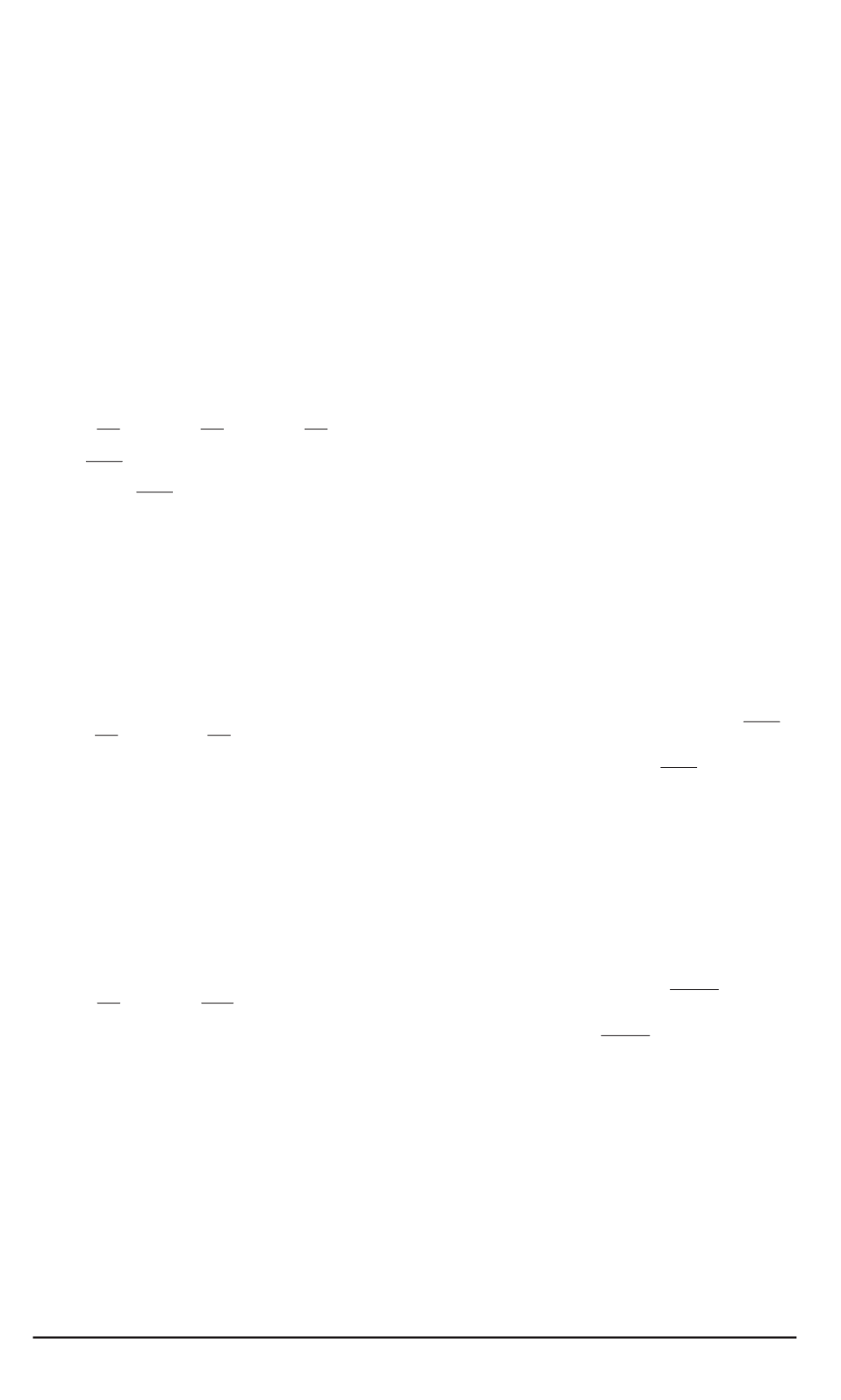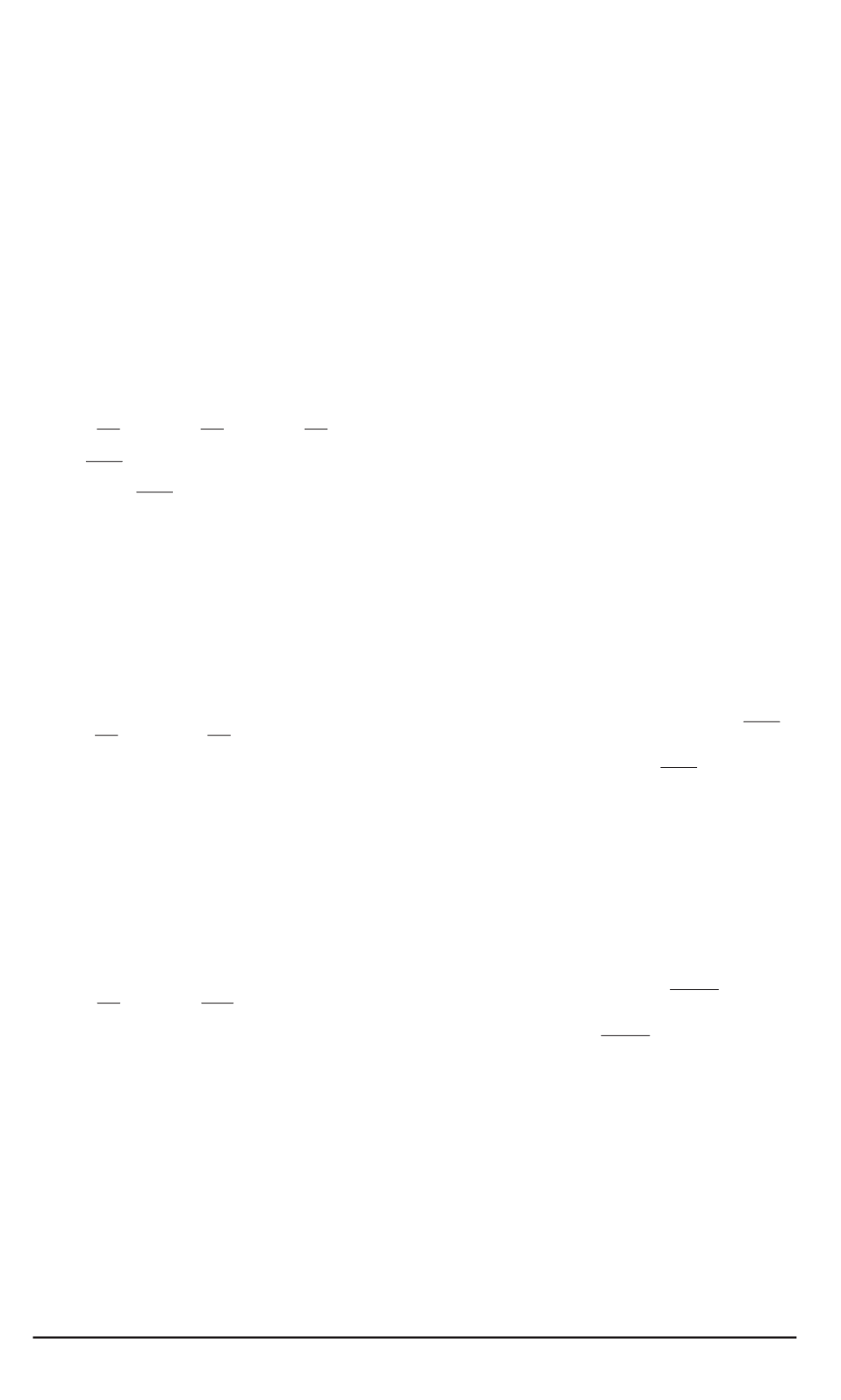
Аэродинамические коэффициенты
p
1
−
p
10
объекта подлежат опреде-
лению по данным аэродинамических продувок в условиях
ϑ
=
α
.
Коэффициент
k
, входящий в
sin(
kα
)
, известен, а парашютная система
испытывается в условиях, когда измеряются
V
x
, V
y
, ω
z
, ϑ
=
α
. Итогом
синтеза будет трехканальный идентификатор:
Канал 1
.
˙˜
V
x
=
h
т
˜
p
−
S
(
ε
)
;
ε
= ˜
V
x
−
V
x
;
˙˜
p
=
−
Kh
Φ(
ε
)
. Здесь
h
= (
V
2
x
+
V
2
y
, V
y
ω
z
, ω
2
z
,
cos
ϑ
)
т
— вектор измерений в момент
t
;
K
=
⎛
⎜⎜⎝
1
ϕ
1
r
12
ϕ
2
r
13
ϕ
3
r
14
ϕ
1
r
12
ϕ
2
1
ϕ
2
ϕ
1
r
23
ϕ
3
ϕ
1
r
24
ϕ
2
r
13
ϕ
2
ϕ
1
r
23
ϕ
2
2
ϕ
3
ϕ
2
r
34
ϕ
3
r
14
ϕ
3
ϕ
1
r
24
ϕ
3
ϕ
2
r
34
ϕ
2
3
⎞
⎟⎟⎠
;
ϕ
1
=
p
2
p
1
,
ϕ
2
=
p
3
p
1
,
ϕ
3
=
p
4
p
1
вычисляются по априорным значениям
p
i
(
i
= 1
,
4)
;
r
ij
— априорные коэффициенты корреляции параметров
p
i
,
p
j
(
i, j
= 1
,
4)
.
Канал 2
.
˙˜
V
y
=
h
т
˜
p
−
S
(
ε
)
;
ε
= ˜
V
y
−
V
y
;
˙˜
p
=
−
Kh
Φ(
ε
)
. Здесь
h
= ((
V
2
x
+
V
2
y
) sin(
kα
)
,
V
x
ω
z
,
sin
ϑ
)
т
— вектор измерений в момент
t
;
K
=
⎛
⎝
1
ϕ
1
r
56
ϕ
2
r
57
ϕ
1
r
56
ϕ
2
1
ϕ
2
ϕ
1
r
67
ϕ
2
r
57
ϕ
2
ϕ
1
r
67
ϕ
2
2
⎞
⎠
;
ϕ
1
=
p
6
p
5
и
ϕ
2
=
p
7
p
5
вычисляются по априорным значениям
p
i
(
i
= 5
,
7)
;
r
ij
— коэффициенты корреляции параметров
p
i
, p
j
(
i, j
= 5
,
7)
.
Канал 3
.
˙˜
ω
z
=
h
т
˜
p
−
S
(
ε
)
;
ε
= ˜
ω
z
−
ω
z
;
˙˜
p
=
−
Kh
Φ(
ε
)
. Здесь
h
= ((
V
2
x
+
V
2
y
) sin(
kα
)
, V
x
ω
z
,
sin
ϑ
)
т
— тот же вектор, что в канале 2.
K
=
⎛
⎝
1
ϕ
1
r
89
ϕ
2
r
810
ϕ
1
r
89
ϕ
2
1
ϕ
2
ϕ
1
r
910
ϕ
2
r
810
ϕ
2
ϕ
1
r
910
ϕ
2
2
⎞
⎠
;
ϕ
1
=
p
9
p
8
,
ϕ
2
=
p
10
p
8
— вычисляются по априорным
p
i
(
i
= 8
,
10)
;
r
ij
—
коэффициенты корреляции параметров
p
i
, p
j
(
i, j
= 8
,
10)
.
Для каждого канала функции
S
и
Φ
необходимо выбирать в соот-
ветствии с теоремой 1.
Пользователю алгоритмом адаптивной идентификации необхо-
димо:
1) ввести в ЦВМ информацию о процессах
V
x
, V
y
, ω
z
, ϑ
;
2) иметь априорные данные о параметрах
р
i
объекта и коэффици-
ентах корреляции
r
ij
;
3) назначить элементы матрицы
K
и усиление регулятора
С
Φ
;
14
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 2