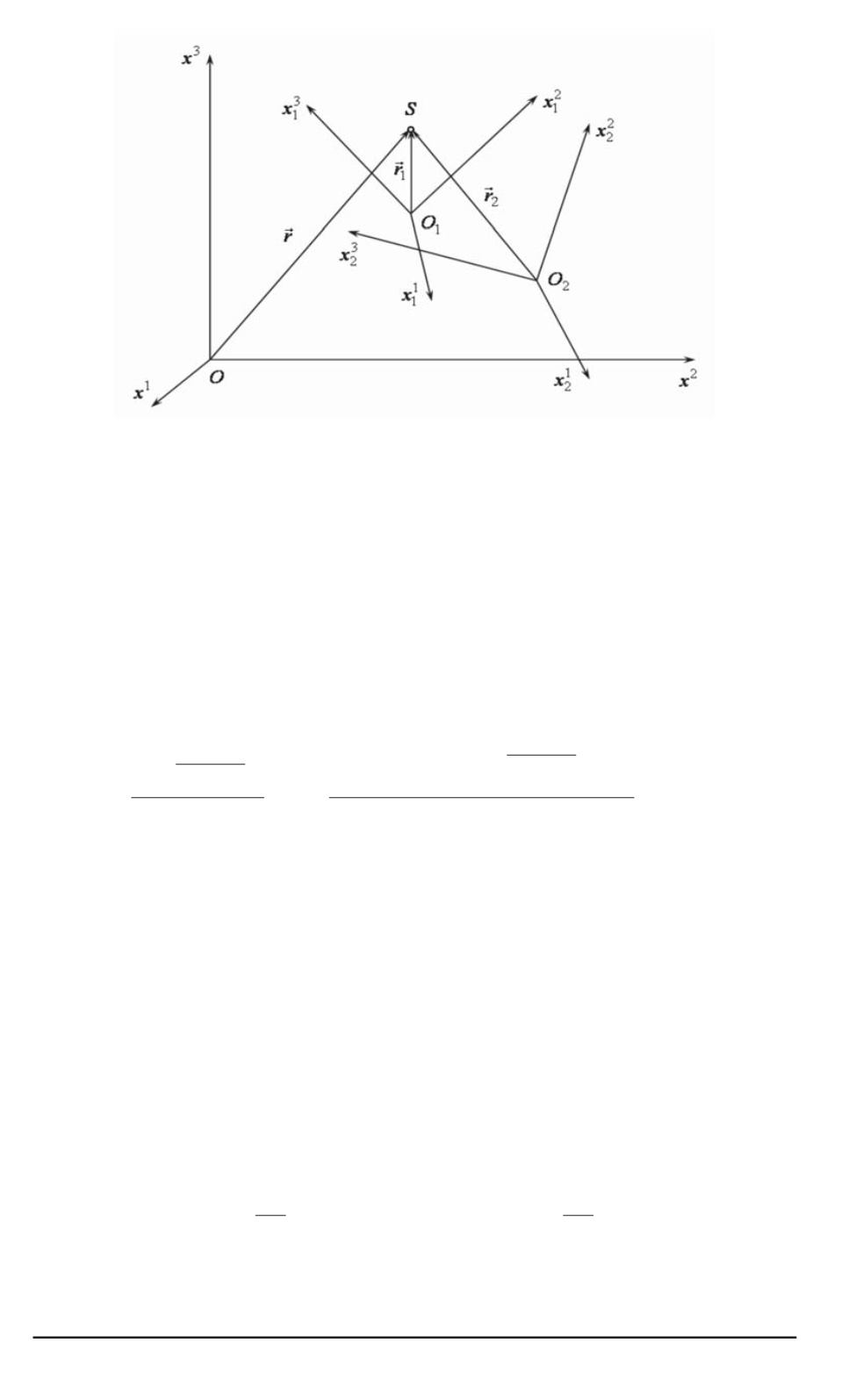
Схема движения ИСО
i
:
ИСО
i
совершают прямолинейное равномерное движение относительно ИСО; любое
событие
S
может быть задано радиус-вектором
r
и временем
t
в ИСО, покоящейся
в ФП
Данные преобразования соответствуют группе Лоренца и облада-
ют инвариантными свойствами для полных дифференциалов. В нее
входят скорости
V
i
, которые связаны формулой преобразования скоро-
сти
β
2
=
aβ
0
+
bβ
1
,
(3)
где
a
=
1
−
β
2
1
1 +
β
1
, β
0
;
b
=
β
1
, β
0
1
−
1
−
β
2
1
+ 1
1 +
β
1
, β
0
;
β
0
=
V
0
/c
;
V
0
— относительная скорость ИСО
1
и ИСО
2
.
Для нахождения преобразований с учетом неинвариантных свойств
частных дифференциалов будем оперировать с дифференциалами ве-
личин, входящих в преобразования (1)–(2), так как частные производ-
ные для выражений полных дифференциалов определяют независи-
мый вклад дифференциалов независимых переменных.
Найдем соотношения для частных дифференциалов простран-
ственных координат.
Получим дифференциал
dr
для (1) при
i
= 1
,
2
и приравняем пра-
вые части полученных выражений, оставив только пространственные
координаты:
D
−
1
1
dr
1
−
V
1
α
1
V
2
1
dr
1
, V
1
=
D
−
1
2
dr
2
−
V
2
α
2
V
2
2
dr
2
, V
2
.
(4)
Уравнение (4) позволяет найти частные производные искомых пре-
образований перед дифференциалами пространственных координат.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 2
19


