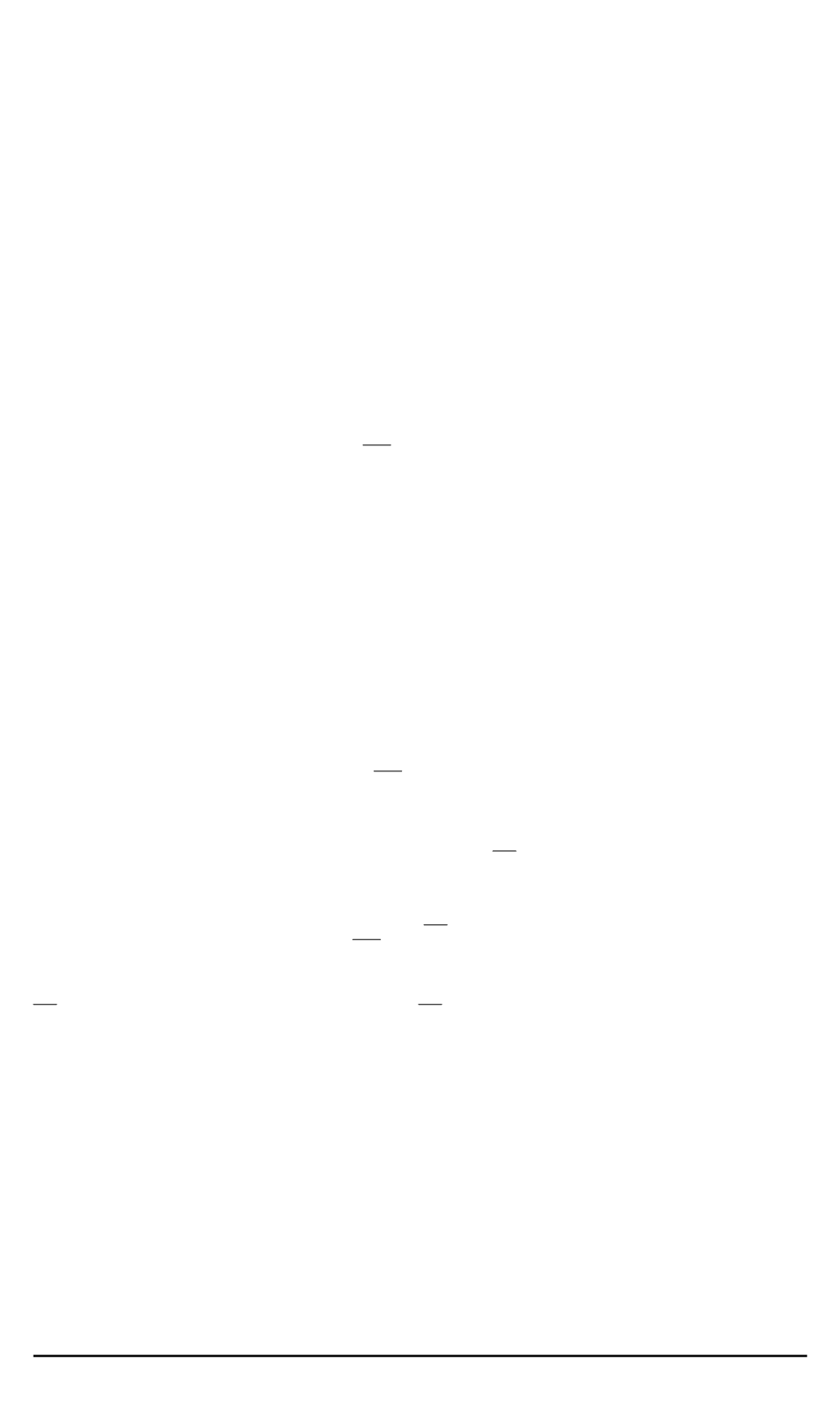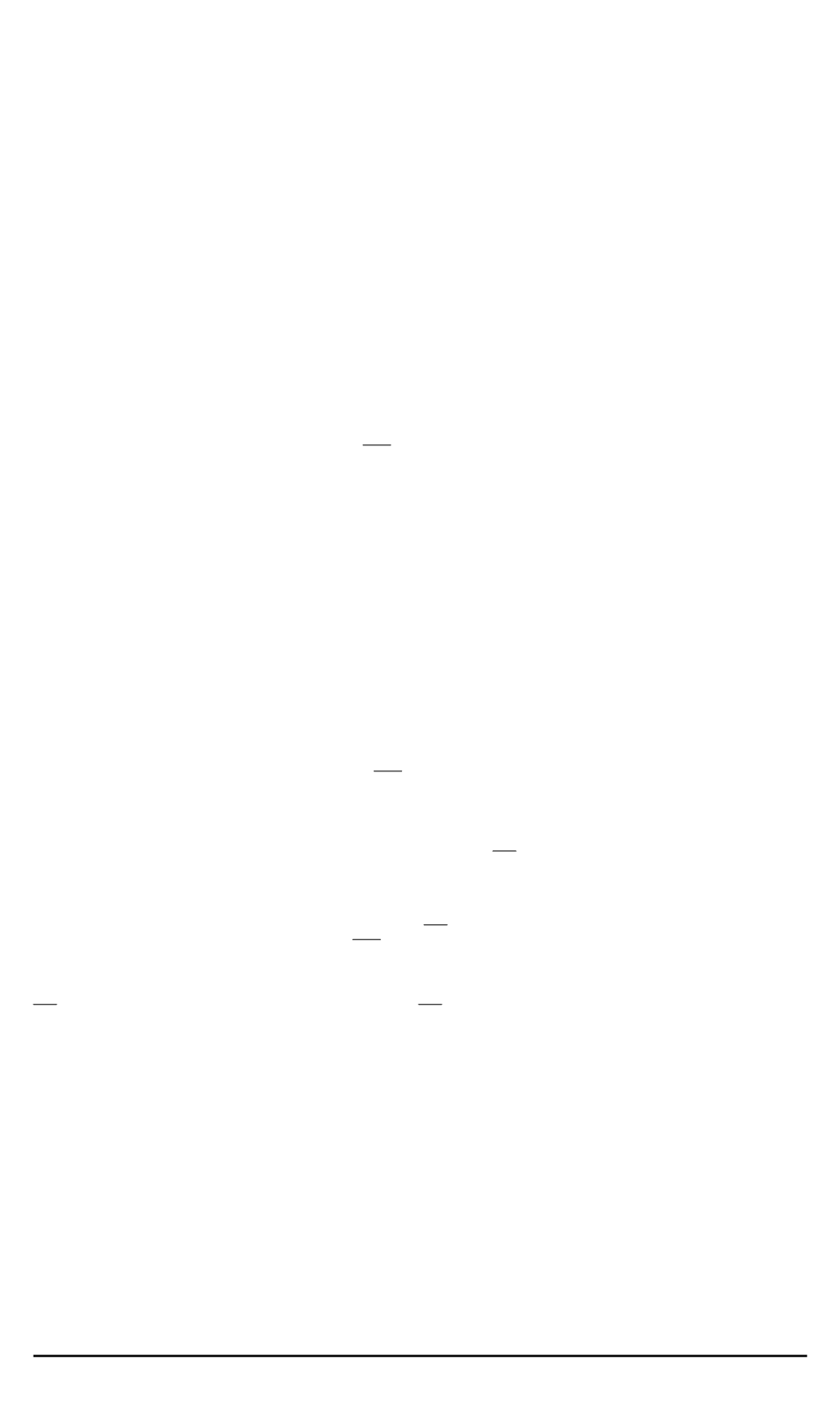
Тогда
k
(
t
) =
n
−
1
X
j
=1
1(
t
)
r
j
(
e
A
т
t
e
1
, e
j
) =
n
−
1
X
j
=1
r
j
k
j
(
t
)
и согласно (5) равенство (4) примет вид
x
1
(
t
) = ˙
ϕ
(
t
) =
n
−
1
X
j
=1
k
j
(
t
−
t
0
)
x
0
j
+
t
Z
t
0
k
(
t
−
τ
)Φ(
ϕ
(
τ
))
dτ.
(6)
Предположим, что все нули функции
S
(
p
)
расположены слева от мни-
мой оси. В этом случае
k
(
t
) =
−
1
2
π
+
∞
Z
−∞
K
(
iω
)
e
iωt
dω.
(7)
Наряду с интегральным уравнением (6) рассмотрим следующее
уравнение:
˙
y
(
t
) =
∞
Z
−∞
ϕ
ω
ср
(
t
−
τ
)Φ(
y
(
τ
))
dτ,
(8)
где
ϕ
ω
ср
(
t
) =
−
1
2
π
ω
ср
Z
−
ω
ср
K
(
iω
)
e
iωt
dω.
Спектр функции
ϕ
ω
ср
(
t
)
обозначим через
K
(
iω
)
:
ϕ
ω
ср
=
1
2
π
∞
Z
−∞
K
(
iω
)
e
iωt
dω,
K
(
iω
) =
−
K
(
iω
)
при
|
ω
| ≤
ω
ср
и
K
(
iω
) = 0
при
|
ω
|
> ω
ср
. Решение
уравнения (6) будем искать в виде
ϕ
(
t
) =
ωt
+
N
X
k
=1
A
k
sin(
kωt
+
γ
k
)
,
(9)
где
ω
= 2
π/T
— частота цикла.
Оказывается, что любое периодическое решение вида (9) уравне-
ния (8) совпадает с периодическими функциями этого вида, найденны-
ми методом квазигармонического баланса, примененным к исходному
уравнению.
6
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 1