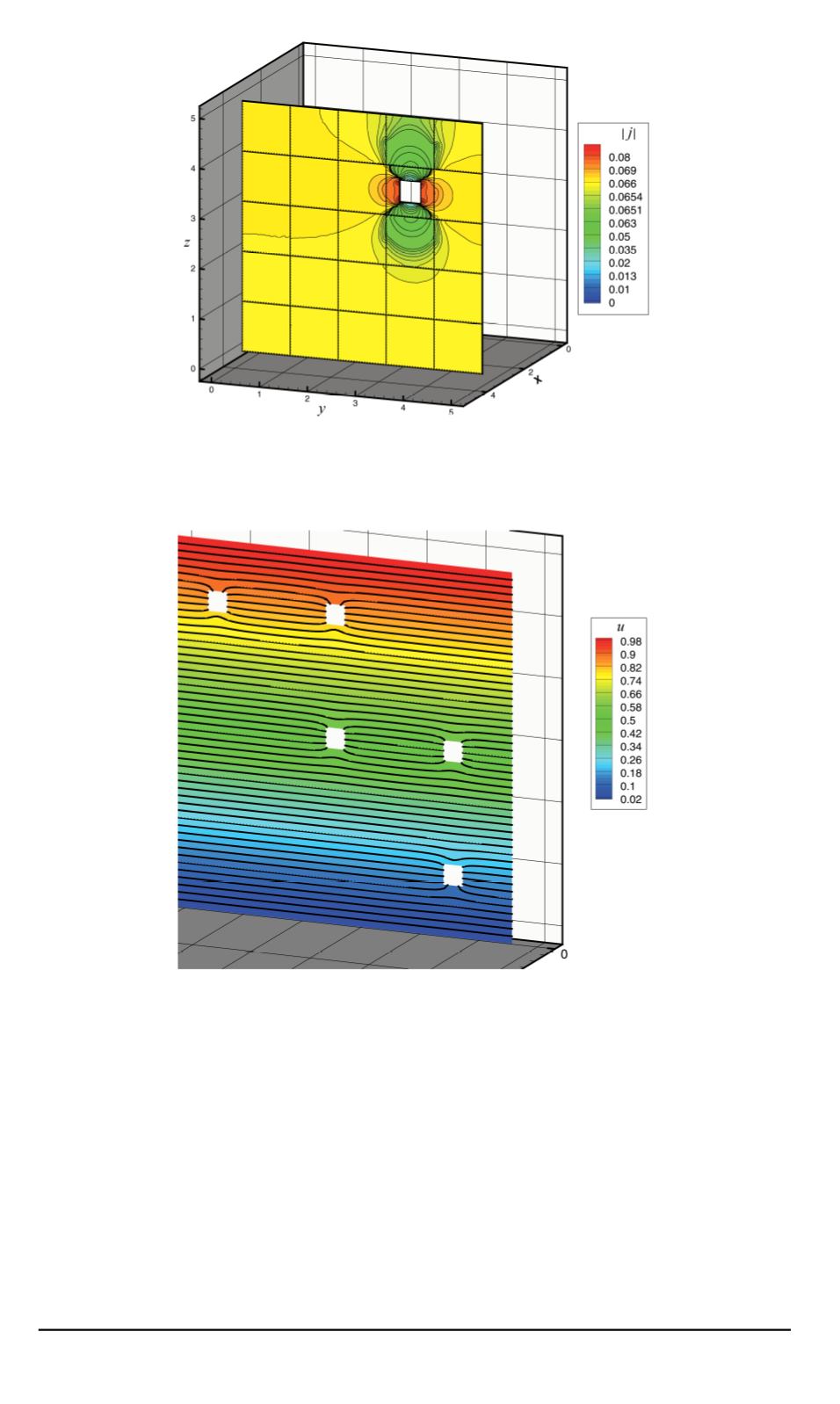
Рис. 1. Плотность электрического тока
|
j
|
в сечении области
x
= 2
,
5
. Области
суперэлементов выделены
Рис. 2. Потенциал
u
(
x, y, z
)
,
x, y, z
2
Ω
в сечении области
x
= 0
,
5
На примере задачи Дирихле исследовано применение МКСЭ Федо-
ренко для решения общих линейных эллиптических задач. Получены
априорные оценки погрешностей метода и установлена его насыщае-
мость в пространствах Соболева. Выведено неравенство Джексона для
МКСЭ-приближений. Приведен пример численного расчета распреде-
ления электрического потенциала в проводящем объекте в трехмерной
постановке.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 2
25


