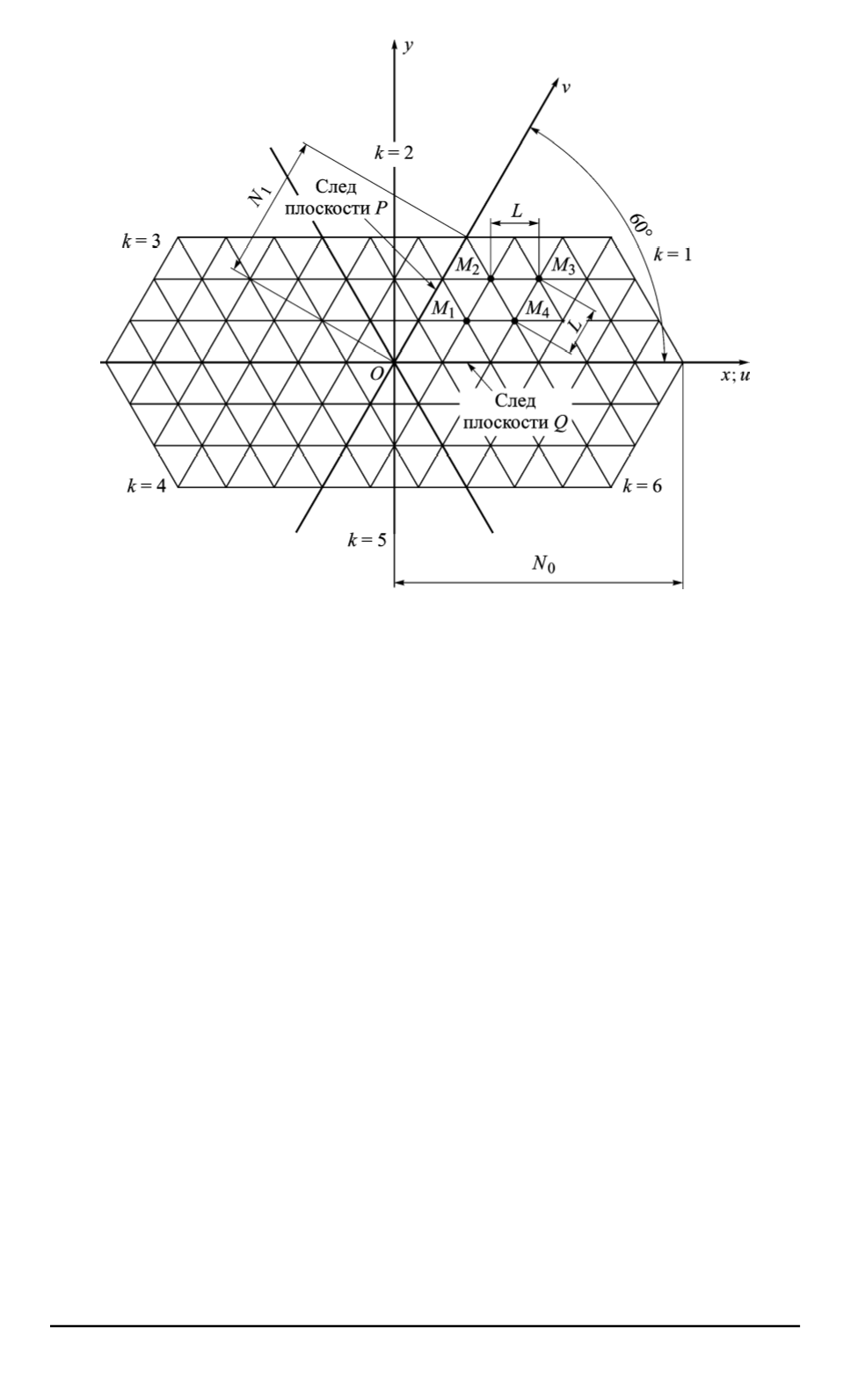
Рис. 2. Отображение лицевого пояса рефлектора на плоскость
Ouv
F
=
{
M
2
R
|
M
p
, p
2
N
∧
[1
, N
уз.л
]
}
,
где
R
,
N
— множества действи-
тельных и натуральных чисел,
а
N
уз.л
=
= 2
N
0
(2
N
1
+ 1)
−
N
1
(
N
1
−
1) + 1
— число узловых шарниров ли-
цевого пояса.
Если в плоскости
Ouv
(рис. 2) определить множество
D
=
=
{
(
u, v
)
2
Z
2
|
(
u
>
−
N
0
∧
u
6
N
0
∧
v
>
N
1
∧
v
6
N
1
∧
v
6
−
u
+
+
N
0
∧
v
>
−
u
−
N
0
)
}
, где
Z
— множество целых чисел, то
F
=
S
(
D
)
,
где
S
:
D →
R
.
Представим
F
в виде
F
=
i
=6
S
i
=1
F
(
s
)
i
S
j
=6
S
j
=1
F
(
r
)
j
, (
i, j
2
N
∧
[1
,
6])
,
где
F
(
s
)
i
=
S
(
D
(
s
)
i
)
,
F
(
r
)
j
=
S
(
D
(
r
)
j
)
,
D
(
s
)
i
=
D ∩ {
(
u, v
)
2
Z
2
|
χ
(1)
k
+2
u
+
χ
(1)
k
+1
v >
0
∧
χ
(1)
k
u
+
χ
(1)
k
−
1
v >
0
}
— множество внутренних точек
i
-го сектора с углом
60
◦
,
D
(
r
)
j
=
D ∩ {
(
u, v
)
2
Z
2
| |
χ
(1)
j
−
1
|
u
+
|
χ
(1)
j
+1
|
v
=0
∧
χ
(1)
j
+1
u
+(
χ
(1)
j
+1
−
χ
(2)
j
)
v >
0
}
— множество точек, принадлежащих
j
-му лучу, представляющему со-
бой границу двух смежных секторов,
χ
(1)
n
=
sign
(sin(
nπ/
3))
, χ
(2)
n
=
sign
(cos(
nπ/
3))
.
Oпределим множество
F
k
=
F
(
s
)
k
S
F
(
r
)
k
S
F
(
r
)
k
0
, где
k
2
N
∧
[1
,
6]
,
k
0
=
k
−
1
, если
k
>
2
, и
k
0
= 6
, если
k
= 1
, которое будем назы-
58
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 4


