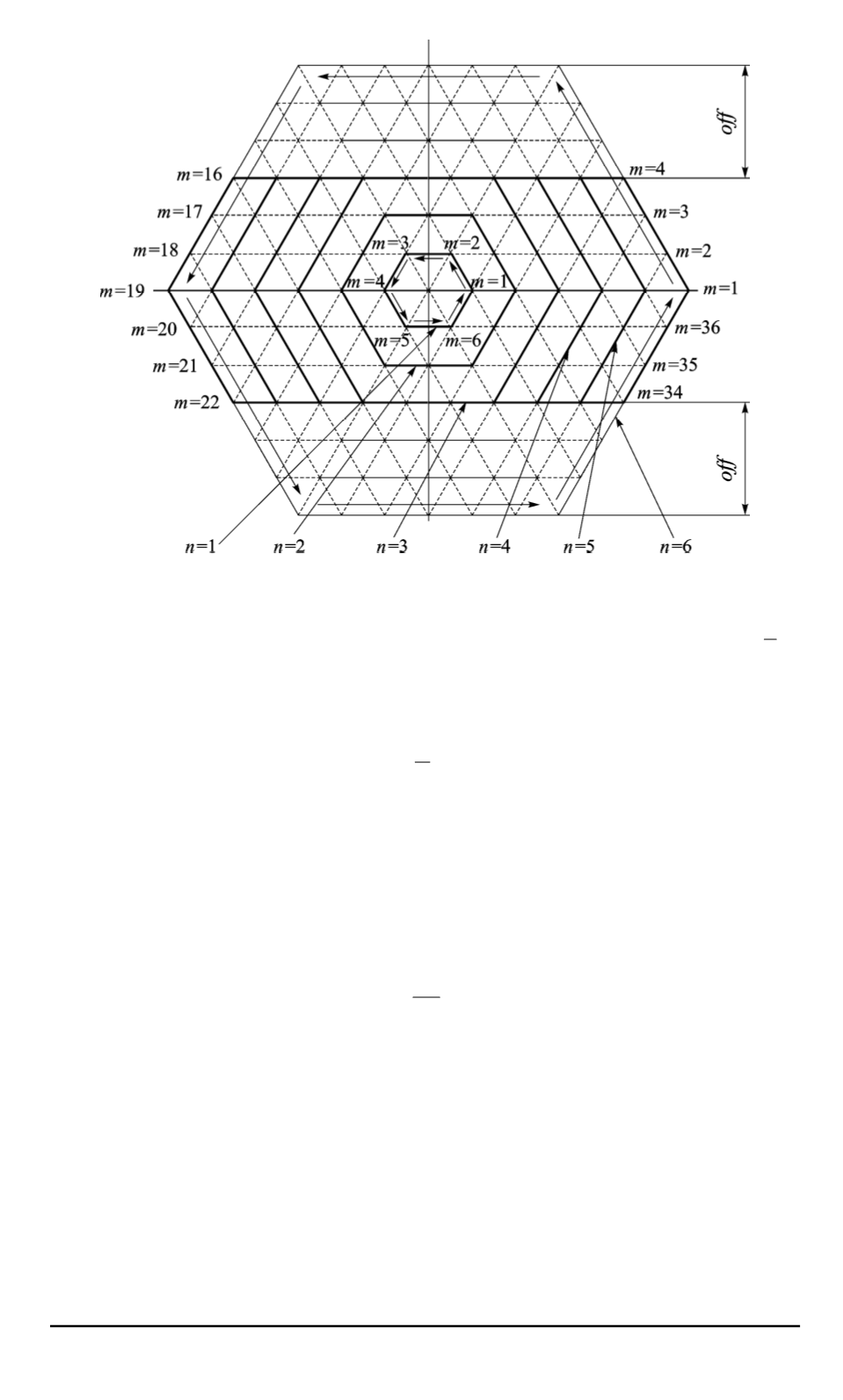
Рис. 4. Полярная целочисленная система координат
если
2
u
+
v >
0
∧
v <
0
;
С
=
π/
2
, если
2
u
+
v
= 0
∧
v >
0
;
С
=
3
2
π
,
если
2
u
+
v
= 0
∧
v <
0
.
Далее определяем номер сектора
k
=
E
3
π
ϕ
0
+ 1
,
где
E
(
. . .
)
— целая часть числа, и соответствующие полярные коорди-
наты:
n
=
|
u
|
+
|
v
|
при
k
= 1
,
4
,
|
v
|
при
k
= 2
,
5
,
|
u
|
при
k
= 3
,
6;
m
=
E
3
n
π
ϕ
0
+ 1
.
Для найденных значений
n
и
m
находим номер центра:
n
ц
=
3
n
(
n
−
1) +
m,
n
6
N
1
,
3
N
1
(
N
1
+ 1) + 2(2
N
1
+ 1)(
n
−
N
1
−
1) +
n
0
, n > N
1
,
(3)
где
n
0
=
m
, если
k
= 1
;
n
0
=
m
−
(3
n
−
2
N
1
−
1)
, если
k
= 3
,
4
;
n
0
=
m
−
2(3
n
−
2
N
1
−
1)
, если
k
= 6
.
Для
k
= 2
,
5
номер
n
ц
определяется по первой зависимости в вы-
ражениях (3), так как для этих секторов
n
6
N
1
.
Приведенные зависи-
мости учитывают, что значения целочисленных полярных координат
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 4
63


