{
α
(0)
p
}
=
cos
ψ
p
sin
ψ
p
0
−
sin
ψ
p
cos
ψ
p
0
0
0 1
,
{
α
(1)
p
}
=
cos
θ
p
0 sin
θ
p
0 1 0
−
sin
θ
p
0 cos
θ
p
,
{
α
(2)
pq
}
=
cos
β
pq
sin
β
pq
0
−
sin
β
pq
cos
β
pq
0
0
0 1
,
где
tg
ψ
p
=
y
p
/x
p
.
Поскольку вектор
τ
p
в точке
M
p
направлен по касательной к кривой
z
p
=
f
(
x
p
)
, то
θ
p
= arctg
df
dx
p
.
Зная угол
ϕ
p
,
можно определить радиус-векторы точек
A
pq
r
A
pq
=
r
1
τ
pq
−
h
1
n
pq
(4)
и направляющие векторы
b
pq
осей цилиндрических шарниров, прохо-
дящих через точки
A
pq
(см. рис. 7). В формуле (4)
r
1
и
h
1
соответствуют
координатам точки
A
pq
в системе координат
M
p
ξ
q
η
q
ζ
q
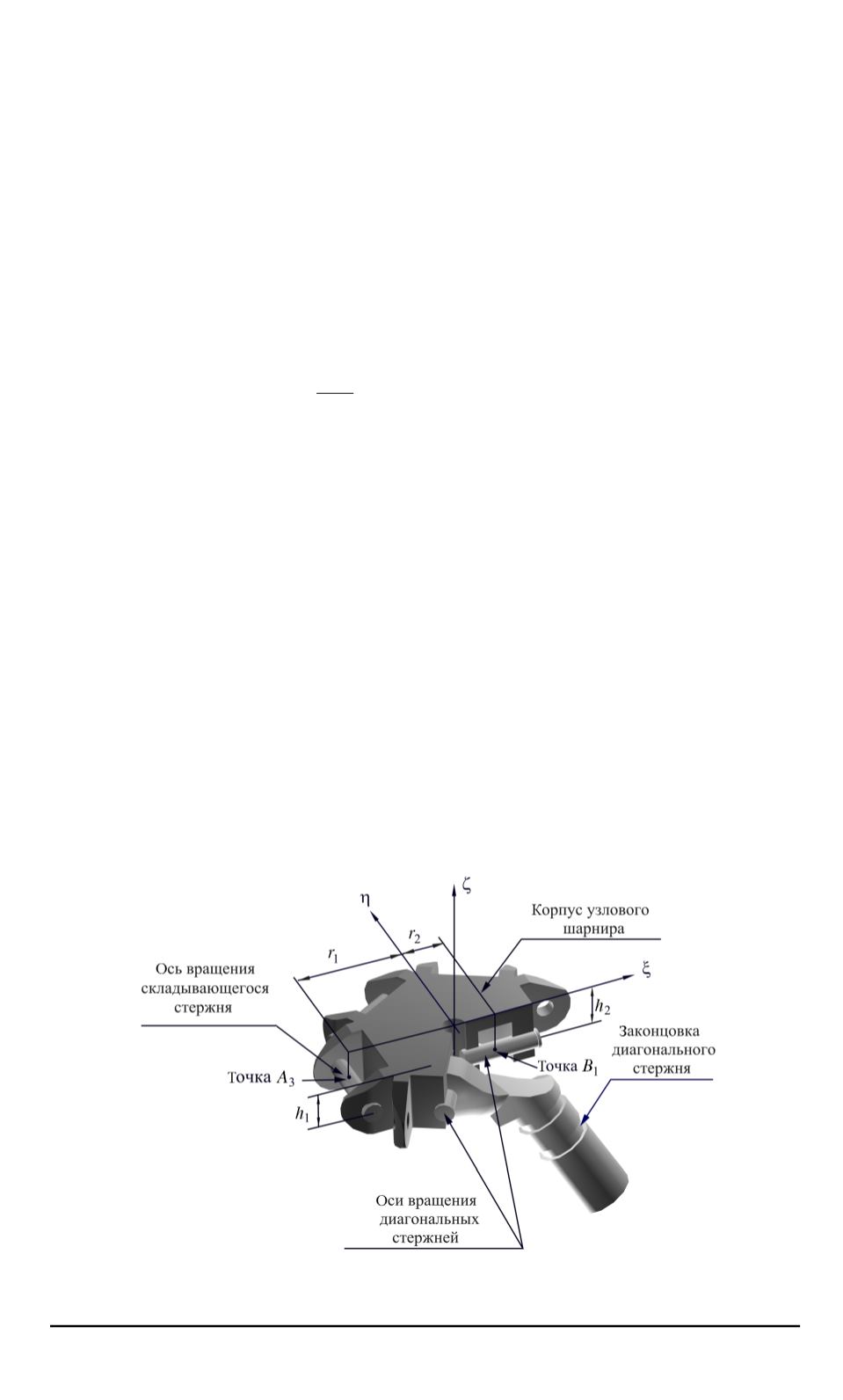
(рис. 8).
После определения положения осей вращения складывающихся
стержней (определено положение систем осей
M
p
ξ
q
η
q
ζ
q
) могут быть
найдены аналогичные геометрические параметры для осей цилиндри-
ческих шарниров трех диагональных стержней, сходящихся в данном
узловом шарнире (см. рис. 8).
Из конструкции узловых шарниров следует, что если направление
координатной оси
M
p
ξ
q
для
q
= 1
определено, то направляющие век-
Рис. 8. Положение осей цилиндрических шарниров диагональных стержней в
узловом шарнире
68
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 4


