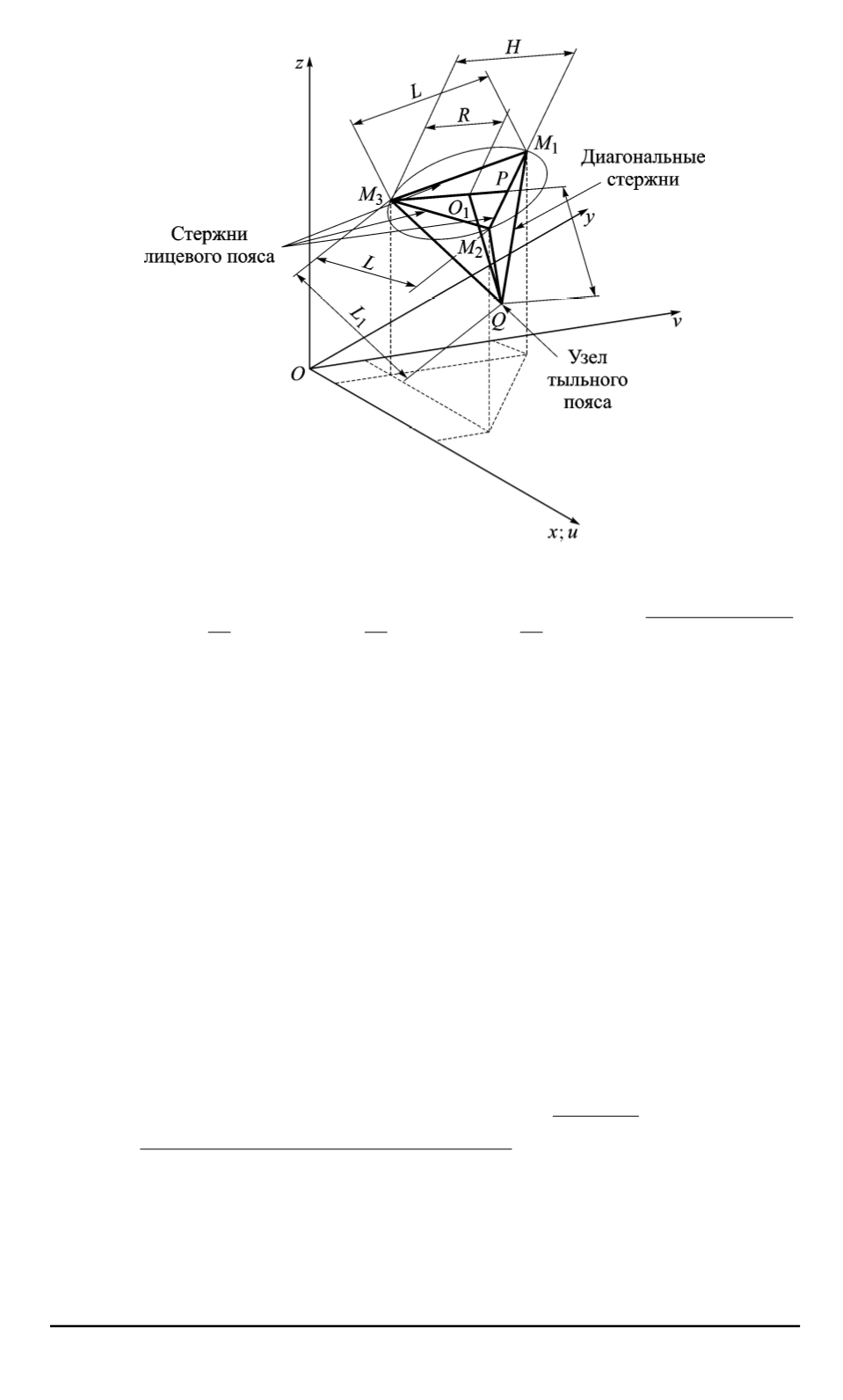
Рис. 3. Элементарная ячейка (тетраэдр) рефлектора
где
cos
α
=
±
A
N
;
cos
β
=
±
B
N
;
cos
γ
=
±
C
N
;
N
=
√
A
2
+
B
2
+
C
2
;
A
= (
y
2
−
y
1
)(
z
3
−
z
1
)
−
(
y
3
−
y
1
)(
z
2
−
z
1
)
;
B
= (
x
3
−
x
1
)(
z
2
−
z
1
)
−
−
(
x
2
−
x
1
)(
z
3
−
z
1
)
;
C
= (
x
2
−
x
1
)(
y
3
−
y
1
)
−
(
x
3
−
x
1
)(
y
2
−
y
1
)
;
i
,
j
,
k
—
орты осей системы координат
Oxyz
;
x
i
, y
i
, z
i
,
i
= 1
,
2
,
3
, — координаты
точек
M
1
, M
2
, M
3
.
Знак в выражении (2) для направляющих косинусов выбирается из
условия расположения центров узловых шарниров тыльного пояса с
внешней стороны образующей поверхности, т.е. должно выполняться
условие
(
n
0
, k
)
<
0
,
где
(
. . . , . . . .
)
означает скалярное произведение векторов.
В этом случае координаты узла
Q
тыльного пояса определяются
по зависимостям (см. рис. 3)
x
Q
=
x
О
1
+
H
1
cos
α, y
Q
=
y
О
1
+
H
1
cos
β, z
Q
=
z
O
1
+
H
1
cos
γ,
где
x
O
1
, y
O
1
, z
O
1
— координаты точки
O
1
;
H
1
=
p
L
2
1
−
R
2
;
R
= 0
,
5
L
2
/H
;
H
=
p
(
x
3
−
x
p
)
2
+ (
y
3
−
y
p
)
2
+ (
z
3
−
z
p
)
2
;
x
p
= 0
,
5(
x
1
+
x
2
)
;
y
p
=
= 0
,
5(
y
1
+
y
2
)
;
z
p
= 0
,
5(
z
1
+
z
2
)
.
В данном случае треугольник
M
1
M
2
M
3
— равнобедренный, что
определяет соответствующие выражения для высоты
H
и радиуса
R
описанной окружности.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 4
61


