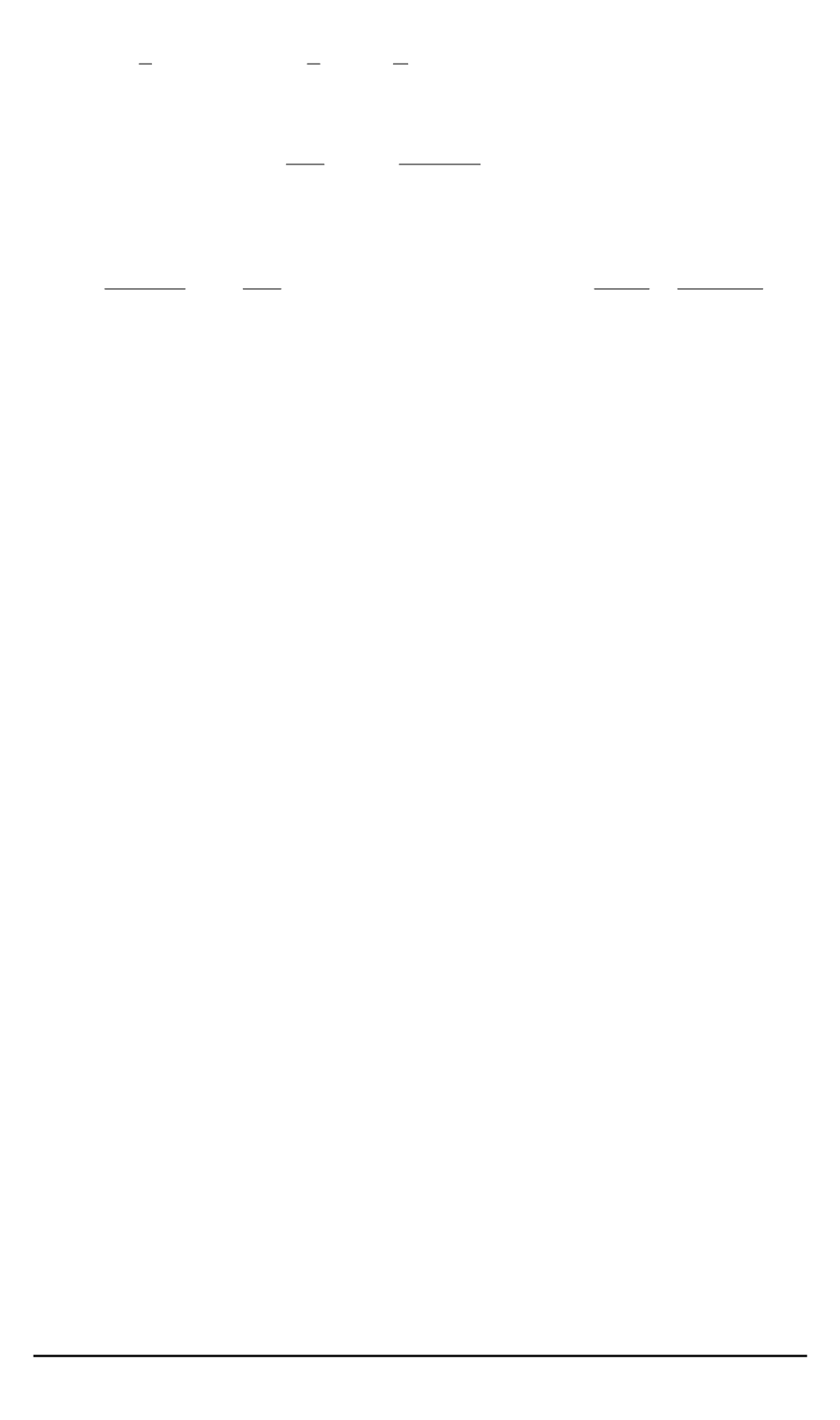
E
d
=
3
2
mv
2
m
f
y
=
3
2
m
λ
τ
2
f
y
=
=
3
8
π
2
m
c
o
k
b
Θ
e
o
~
k
1
/
3
p
!
2
f
y
=
E
d
1
f
y
=
C
ld
E
L
,
(32)
где обозначено
C
ld
=
3
k
o
n
2
π
2
k
2
/
3
p
=
9
8
π
2
C
D
, E
d
1
=
E
d
(
f
y
= 1) =
3
m
8
k
2
/
3
p
3
c
o
k
b
Θ
o
4
π
~
2
.
(33)
Здесь функция
f
y
отражает тот факт, что в общем случае классиче-
ская величина предела интегрирования
E
d
1
/k
b
T
должна быть замене-
на отношением
E
d
/
(2
h
E
k
i
)
, где
h
E
k
i
— средняя кинетическая энергия,
приходящаяся на одну степень свободы атома системы. В классиче-
ском случае
h
E
k
i
=
k
b
T/
2
. Однако с учетом квантовых эффектов (а
делокализация — это переход от квантового движения атома в ячейке
к классическому переносу по всему объему системы), следует ввести
множитель
f
y
=
k
b
T/
(2
h
E
k
i
)
.
Отметим, что выражения (30), (31) и (32), полностью удовлетворя-
ют как условию согласованности термического и калорического урав-
нений состояния, так и третьему началу термодинамики в “сильной”
формулировке Планка [1]. Конкретные расчеты температуры Дебая по
(30) и активационных параметров по (31) и (32) показали хорошее
согласие с экспериментальными данными для различных простых ве-
ществ: с разным типом химической связи, различной структурой и с
разным изотопным составом. Было показано, что они применимы и к
квантовым кристаллам, и при любых значениях давления.
Расчеты изотерм уравнения состояния аргона.
Для проведе-
ния расчетов уравнения состояния
P
=
−
(
∂f/∂v
)
T
был взят аргон
(
m
= 39
,
95
а.е.м), имеющий в твердой фазе ГЦК-структуру (
k
o
n
= 12
).
Параметры межатомного потенциала Ми–Леннарда–Джонса для арго-
на приняты в виде [1]
r
o
= 3
,
7555
∙
10
−
10
м
, D/k
b
= 173
,
6
K
, a
= 6
, b
= 17
.
При этом входящие в формализм термодинамические константы мо-
дели равны
v
o
= (
π/
6
k
p
)
r
3
o
= 37
,
4522
∙
10
−
30
м
3
,
V
o
=
v
o
N
A
= 22
,
5542
cм
3
/
моль
,
Θ(
c/r
o
= 1) = 86
,
807
K
.
Отметим, что эти параметры межатомного потенциала (18) опре-
делены из экспериментальных данных для кристаллов при
T
= 0
K и
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 2
37


