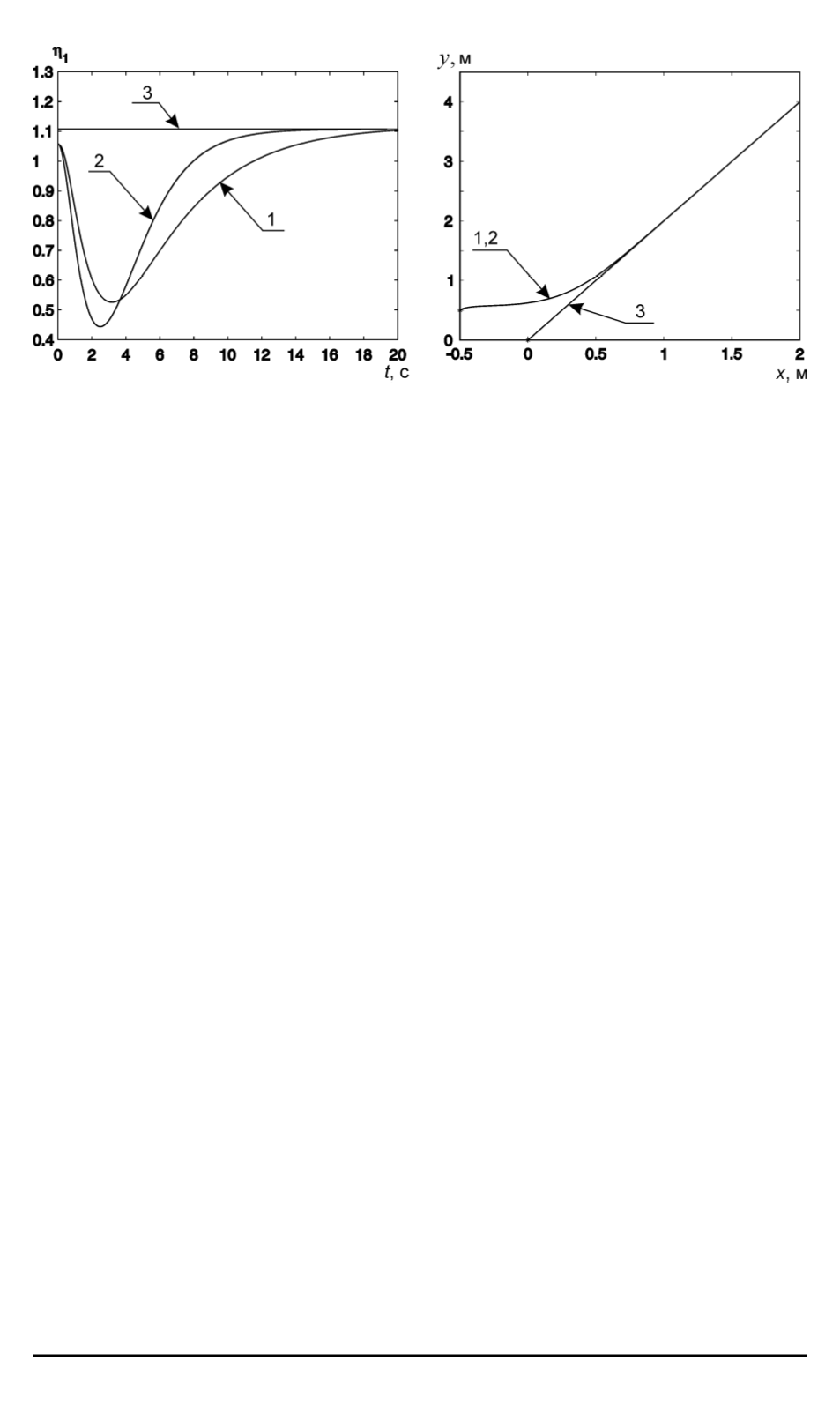
Рис. 7. Сравнение траекторий движения (
1
— траектория “велосипедной” моде-
ли,
2
— траектория “четырехколесной” модели,
3
— программная траектория)
На рис. 7 приведены графики изменения переменной
η
1
для двух
моделей, а также программная и реализующиеся линии движения на
плоскости. Можно видеть, что для “четырехколесной” модели стаби-
лизация по переменной
η
1
=
ψ
происходит быстрее, что соответствует
более естественному выезду на заданную линию движения, в то время
как для “велосипедной модели” имеется участок, где реализуется дви-
жение вдоль прямой линии, при котором продольная ось симметрии
робота имеет небольшой угол с линией движения. Реализующиеся
линии движения центров масс обеих моделей совпадают, поскольку
имеют место одинаковые отклонения и применяется одинаковая ста-
билизирующая обратная связь.
Выводы.
Разработанная методика позволяет получить програм-
мные управления и управления в виде обратных связей, решающие
задачу отслеживания программной траектории движения робота. Про-
граммную траекторию можно строить на основе пары параметри-
ческих сплайнов
p
x
(
τ
)
,
p
y
(
τ
)
, которые задают на плоскости линию
движения, проходящую через заданные точки, и профиля скорости
τ
=
f
(
t
)
.
Предположения о малости углов скольжения и углов поворота ко-
лес накладывают ограничения на класс траекторий, поскольку кривиз-
на траектории и заданный профиль скорости определяют реализую-
щиеся углы.
Работа выполнена при финансовой поддержке гранта РФФИ
№ 06-07-89265 и программы Минобрнауки “Развитие научного по-
тенциала высшей школы на 2006–2007 гг.”
54
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


