ем заданных зависимостей
z
1
(
t
)
,
z
2
(
t
)
и вычисленных значений
η
1
,
η
2
получаем
u
1
и
u
2
, что позволяет проинтегрировать последние два
уравнения на следующем шаге.
Отметим, что устойчивость уравнений нулевой динамики системы
в отклонениях от заданного программного движения удается исследо-
вать только численно.
Исследование устойчивости нулевой динамики.
Пример 1.
Рас-
смотрим “велосипедную” модель со следующими параметрами [2]:
m
= 150
кг,
J
= 82
кг
∙
м
2
,
l
r
= 0
,
4
м,
l
f
= 0
,
6
м. Коэффициенты
c
f
и
c
r
примем равными 4480 и 6720 Н/рад соответственно, что соответствует
хорошему сцеплению колес с поверхностью.
Рассмотрим программную траекторию по переменным
x
и
y
, за-
данную в виде
x
=
x
(
t
) =
z
1
(
t
) =
a
sin(
ωt
);
y
=
y
(
t
) =
z
3
(
t
) =
b
cos(
ωt
)
,
(37)
где
a
= 4
,
5
м,
b
= 3
м,
ω
=
π/
10
,
t
2
[0
,
10]
.
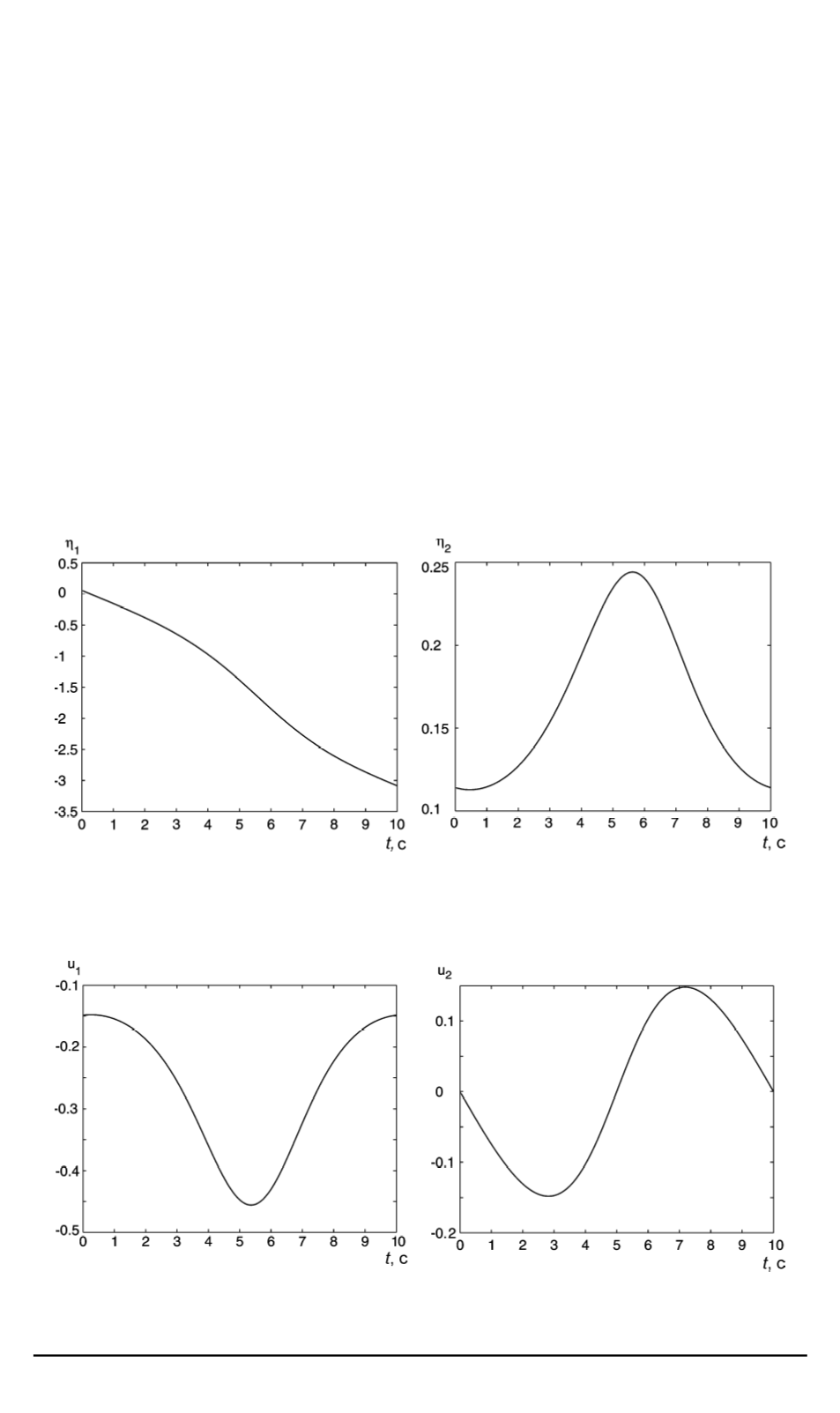
Рис. 3. Программная траектория для переменных
η
1
,
η
2
Рис. 4. Графики программных управлений
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
51


