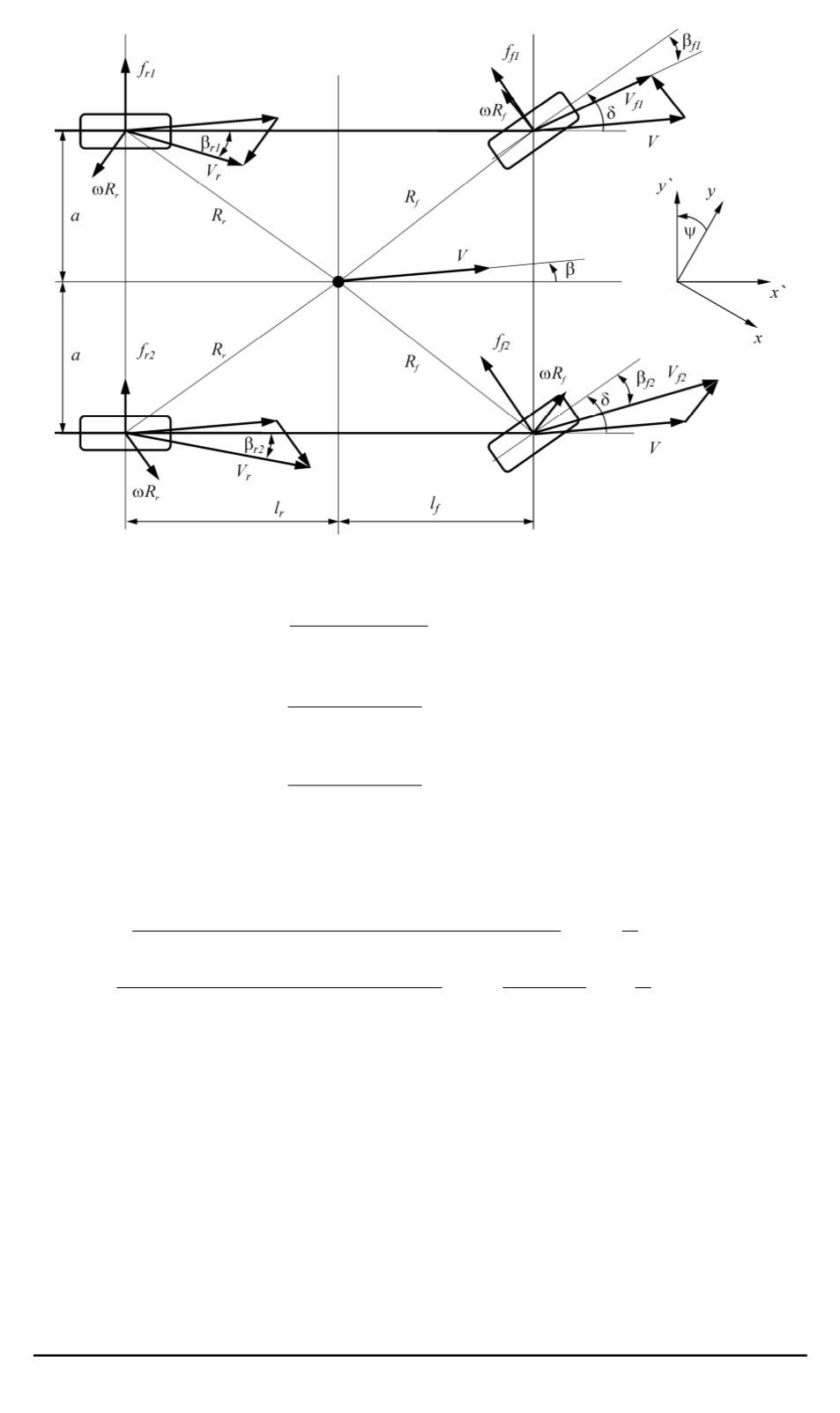
Рис. 2. “Четырехколесная” модель мобильного робота
β
f
2
= arctg
v
sin
β
+
l
f
ω
v
cos
β
+
l
f
ω
−
δ
=
α
f
2
(
v, β, ω
)
−
δ
;
β
r
1
= arctg
v
sin
β
−
l
r
ω
v
cos
β
−
aω
=
α
r
1
(
v, β, ω
);
β
r
2
= arctg
v
sin
β
−
l
r
ω
v
cos
β
+
aω
=
α
r
2
(
v, β, ω
)
.
В предположении о малости угла скольжения и угла поворота пе-
редних колес получим
˙
β
=
−
c
f
1
(
α
f
1
−
δ
)+
c
f
2
(
α
f
2
−
δ
)+
c
r
1
α
r
1
+
c
r
2
α
r
2
mv
−
ω
−
β
v
˙
v
=
=
−
c
f
1
α
f
1
+
c
f
2
α
f
2
+
c
r
1
α
r
1
+
c
r
2
α
r
2
mv
−
ω
+
c
f
1
+
c
f
2
mv
u
1
−
β
v
u
2
;
J
˙
ω
=
−
(
c
f
1
(
α
f
1
−
δ
) +
c
f
2
(
α
f
2
−
δ
))
l
f
+ (
c
f
2
(
α
f
2
−
δ
)
−
−
c
f
1
(
α
f
1
−
δ
))
aδ
+ +(
c
r
1
α
r
1
+
c
r
2
α
r
2
)
l
r
=
=
−
(
c
f
1
α
f
1
+
c
f
2
α
f
2
)
l
f
+ (
c
f
2
α
f
2
−
c
f
1
α
f
1
)
au
1
+
+(
c
r
1
α
r
1
+
c
r
2
α
r
2
)
l
r
+ (
c
f
1
+
c
f
2
)
l
f
u
1
+ (
c
f
1
−
c
f
2
)
au
2
1
;
˙
v
=
u
2
;
˙
ψ
=
ω
;
˙
x
=
v
cos(
β
+
ψ
);
˙
y
=
v
sin(
β
+
ψ
)
.
(33)
48
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


