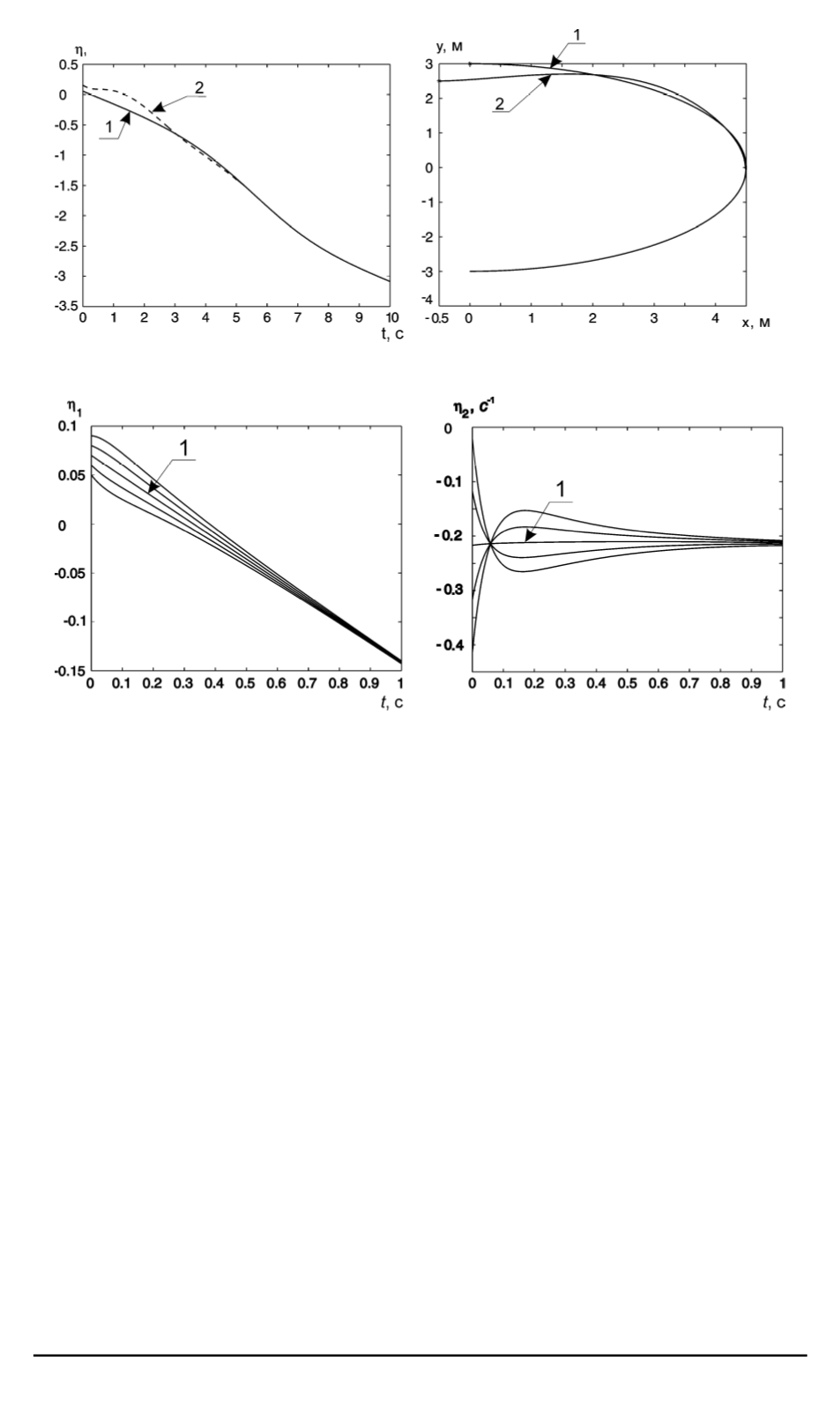
Рис. 5. Пример стабилизации программной (
1
) и реализующейся (
2
) траекторий
Рис. 6. Исследование устойчивости нулевой динамики (
1
— программная траек-
тория)
значений от программных значений
η
1
(0)
и
η
2
(0)
. Из графиков мож-
но видеть, что нулевая динамика “четырехколесной” модели является
асимптотически устойчивой.
Для детального исследования свойств нулевой динамики “четы-
рехколесной” модели можно использовать свойства нулевой динамики
“велосипедной” модели. В этом случае нулевая динамика “велосипед-
ной” модели, записанная в переменных (34) линейная, стационарная
и асимптотически устойчивая при
v
(
t
) =
v
0
. Построив стационар-
ную функцию Ляпунова, ее можно использовать для доказательства
равномерной асимптотической устойчивости нулевой динамики “че-
тырехколесной” модели.
Сравнение свойств моделей.
На численном примере сравним
свойства “велосипедной” и “четырехколесной” моделей. Примем
z
1
(
t
) = 0
,
1
t
;
z
3
(
t
) = 0
,
2
t.
Стартовую точку, лежащую вне программной траектории, зададим
одинаковой для обеих моделей. Одинаковые начальные значения при-
своим остальным переменным и параметрам моделей.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
53


