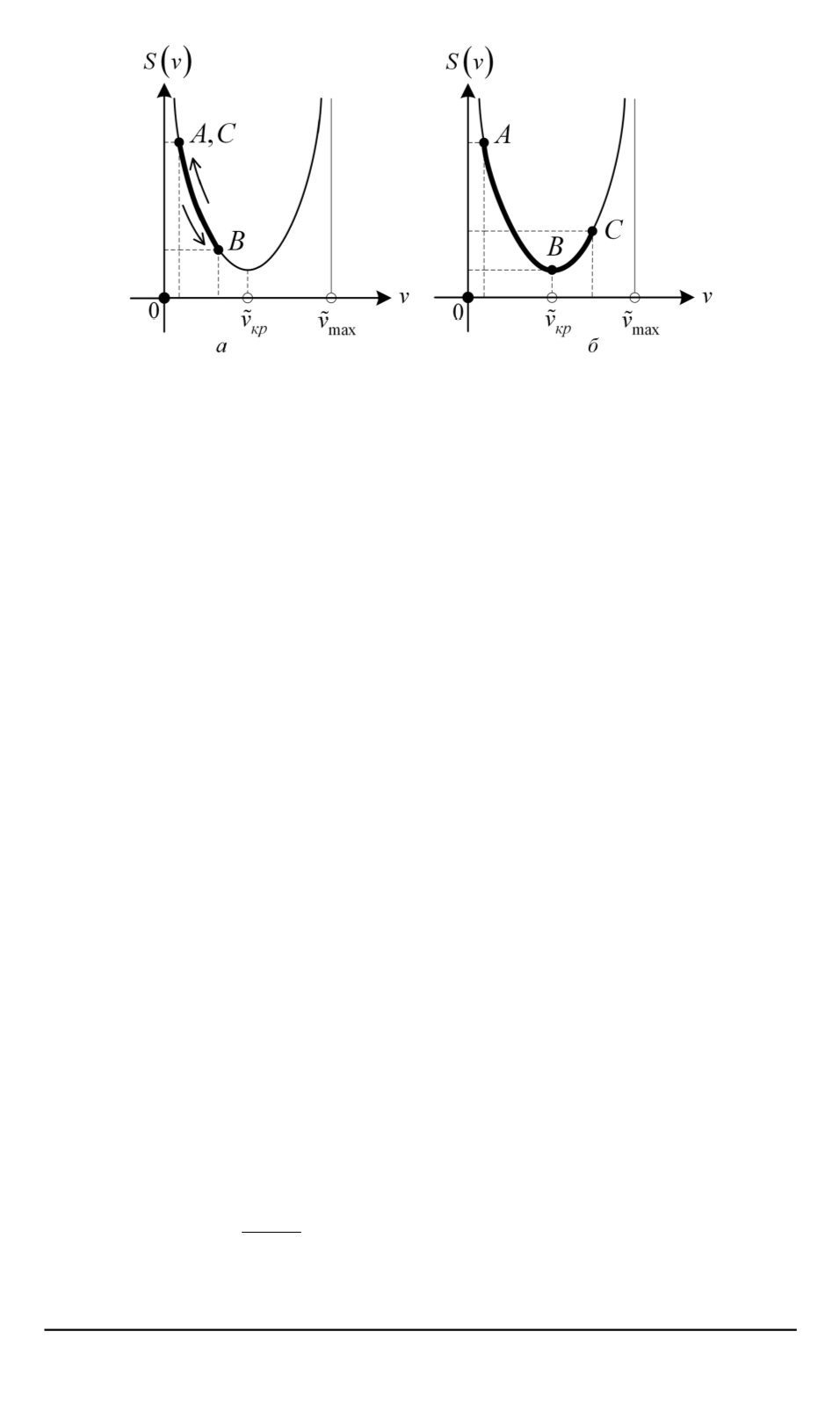
Рис. 3. Решения для дозвукового (
а
) и сверхзвукового (
б
) течения
задачи (10) — для дозвукового и сверхзвукового течения. Для рассмо-
трения этих решений рассмотрим третье уравнение в (27), из которого
следует, что
S
(
v
) = ˉ
M
|
V
ξg
|
F
(
v
)
D
˜
F
(
v
)
E
g
.
v.
(28)
Функция зависимости площади сечения
S
поровой области
V
ξg
от модуля скорости
v
имеет локальный минимум в точке
v
= ˜
v
кр
=
= [(
γ
−
1)
/
(
γ
+ 1)]
1
/
2
˜
ν
max
(левее и правее которой ветви кривой напра-
влены вверх, пересечений с осью абсцисс нет) и две асимптоты:
v
= 0
и
v
= ˜
v
max
.
Если в поре реализуется дозвуковой режим течения, то скорости
частиц жидкости лежат на левой ветви кривой
S
(
v
)
, газодинамиче-
ские параметры — периодические функции локальной координаты
z
(рис. 3,
а
). Если же в поре течение становится сверхзвуковым, то пе-
риодического решения локальной задачи (10) не существует. Иначе
говоря, трансзвуковое решение является переходным. Наличие пере-
хода определяется значением массового расхода
ˉ
Q
и функцией
S
(
z
)
.
Численный метод решения локальной задачи.
Для численного
решения системы уравнений (27), фактически представляющей со-
бой нелинейное интегральное уравнение относительно функции
v
(
z
)
,
введем на отрезке
[
−
1
/
2; 1
/
2]
оси
Oz
сетку узлов
z
m
=
−
1
/
2 +
+
m/n, m
= 0
, . . . , n
,
n
— целое число. Тогда разностная аппрокси-
мация оператора осреднения (8) для случая функции
Ω(
z
)
, зависящей
только от
z
, будет иметь следующий вид:
h
Ω
i ≈
πh
2
|
V
ξg
|
n
X
m
=1
Ω
m
−
1
f
2
Σ
(
z
m
−
1
) + Ω
m
f
2
Σ
(
z
m
)
,
(29)
где
h
=
z
m
−
z
m
−
1
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1
33


