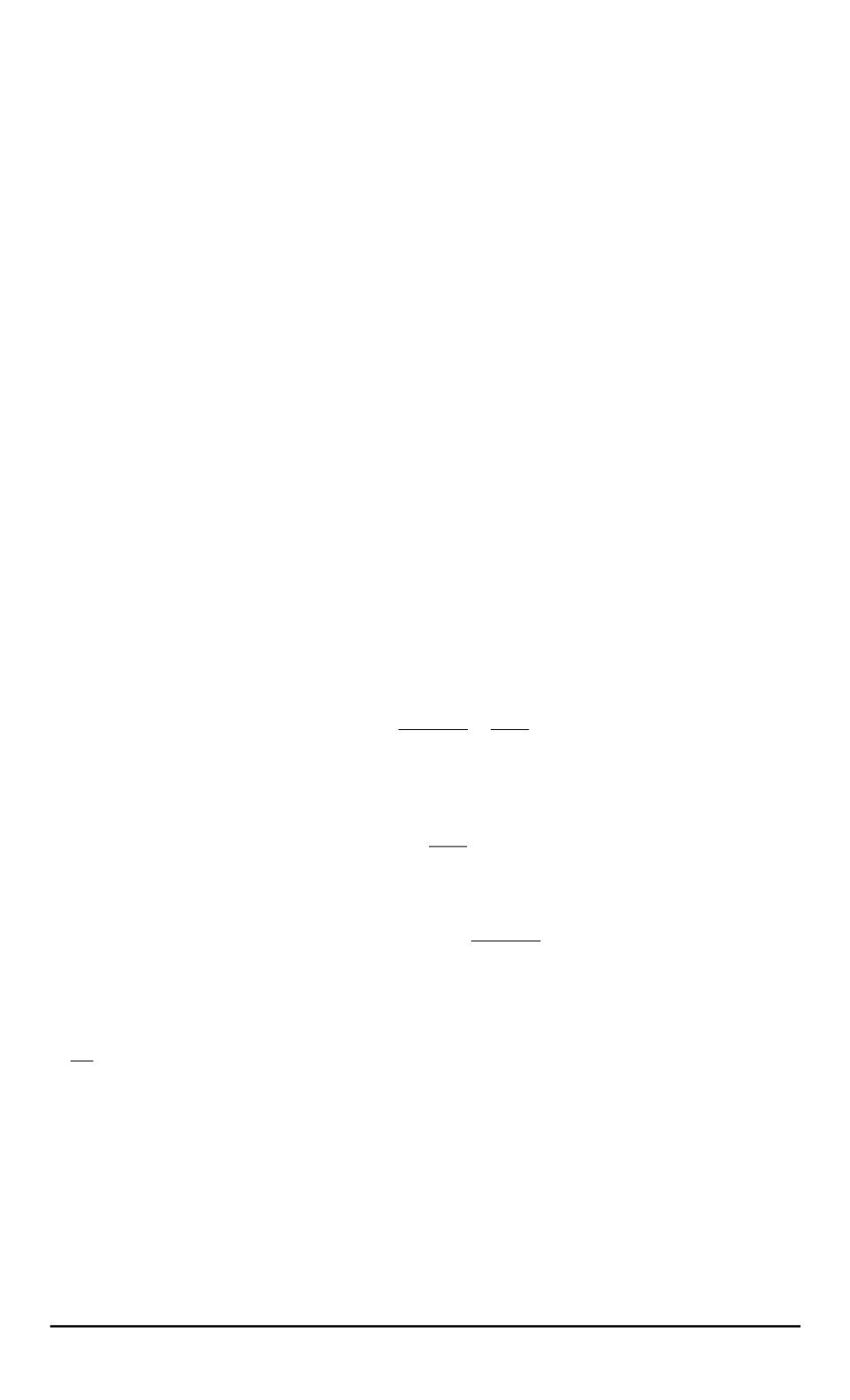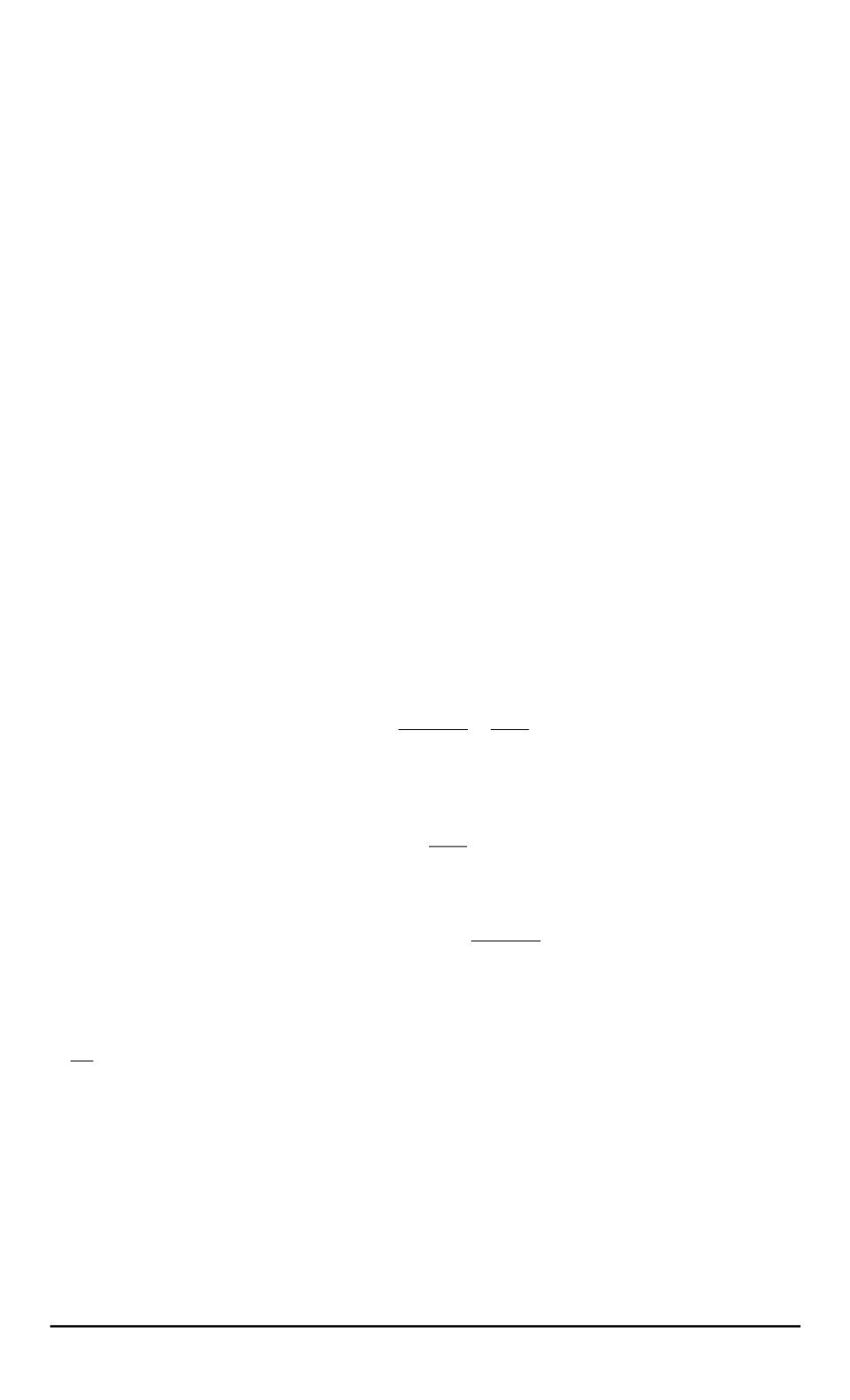
могут быть минимизированы одновременно. Необходимо найти ком-
промисс, который мог бы быть легко достигнут при помощи линейной
комбинации двух функций
J
(x) =
J
1
(x) +
λJ
2
(x)
.
(6)
Скаляр
λ
— это параметр регуляризации, регулирующий соотношение
между
J
1
(x)
и
J
2
(x)
. Если
λ
= 0
, то получается нерегуляризованное
решение. Если
λ
велико, решение определяется априорной информа-
цией об
x
. В общем случае выбор подходящего
λ
связан с особенно-
стями решаемой задачи и является нетривиальным.
Один из наиболее широко известных подходов к регуляризации
предложен Тихоновым [10]. Алгоритм Тихонова предполагает, что
норма решения должна быть малой, это ограничивает коэффициент
усиления в соответствии с малыми собственными числами. Целевая
функция принимает вид
J
(x) =
k
Tx
−
y
k
2
2
+
λ
k
x
k
2
2
.
(7)
Здесь норма разности
`
2
есть условие близости к данным измерений
J
1
(x)
, а
k
x
k
2
2
играет роль
J
2
(x)
из соотношения (6). Значение оценки
ˆx
, доставляющее минимум целевой функции (7), может быть вычи-
слено по следующей формуле [10]:
ˆx =
K
X
i
=1
σ
2
i
σ
2
i
+
λ
u
0
i
y
σ
i
v
i
.
(8)
Другие алгоритмы квадратичной регуляризации основаны на соот-
ношении из работы [11]
ˆx =
K
X
i
=1
w
i
u
0
i
y
σ
i
v
i
. Они могут рассматриваться
как взвешенные псевдообращения с весами
w
i
. Регуляризация Тихо-
нова — это частный случай при
w
i
=
σ
2
i
σ
2
i
+
λ
. Идея всех указанных
алгоритмов заключается в том, что большинство больших собствен-
ных чисел оставляют неизменными и ограничивают влияние малень-
ких собственных чисел матрицы
T
, поскольку помеха усиливается в
√
N
раз в направлении собственного вектора, соответствующего наи-
меньшему собственному числу (здесь
N
— отношение наибольшего
собственного числа матрицы
T
к наименьшему). Алгоритмы квадра-
тичной регуляризации очень удобны во многих практических задачах,
и их преимущество состоит в том, что решение имеет короткую ана-
литическую запись. Однако, так как обратный оператор всегда явля-
ется линейной функцией измерений, имеют место некоторые ограни-
чения. В частности, в связи с линейностью невозможно восстановить
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3
9