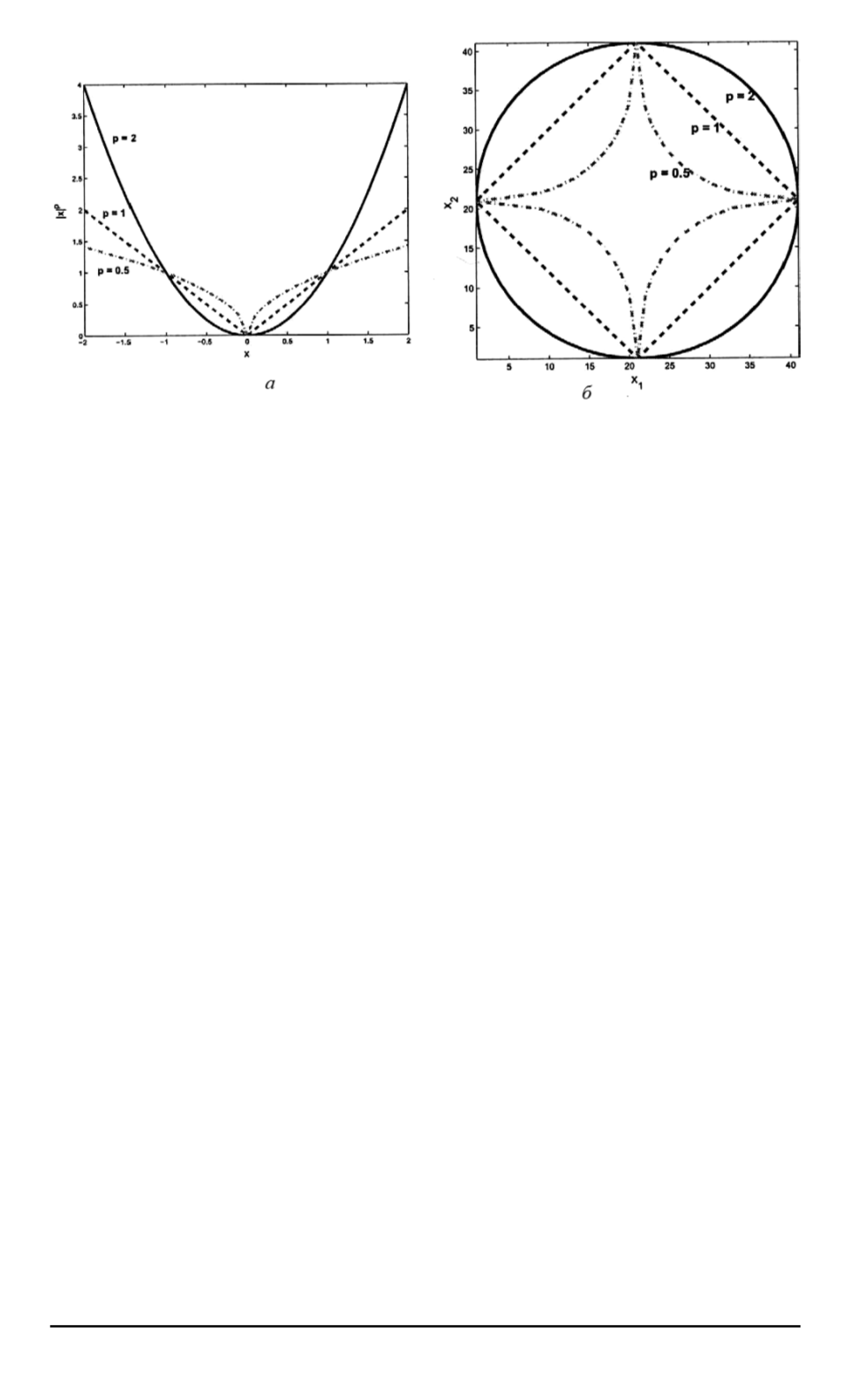
Рис. 2. Одномерный график
k
x
k
p
p
при
p
= 50
,
5
; 1; 2 (
а
) и двумерное множество
уровней
k
x
k
p
p
при тех же
p
(
б
)
в одномерном случае, т.е. то, что штраф на большие составляющие
(большие
x
i
)
уменьшается с уменьшением
p
. Мощные составляющие
штрафуются намного меньше при
`
p
-штрафовании с
p
6
1
, чем при
`
2
-штрафовании (регуляризация Тихонова). Этим объясняется сглажи-
вающий эффект
`
2
-штрафования.
Другой вывод, который можно сделать из рис. 2 — это то, что
`
1
-норма — выпуклая, тогда как при
p
6
1
`
p
-норма уже не вы-
пукла. При
p
6
1
неравенство треугольника не выполняется, и более
справедливо применить термин “квазинорма” вместо термина “нор-
ма”. Однако термин
`
p
-норма будет использован для любого значе-
ния
p
. Вычислительная процедура минимизации нескольких невыпу-
клых регуляризирующих функций (в частности
`
p
)
может быть упро-
щена при использовании полуквадратичного алгоритма регуляризации
[17]. Ключевая идея состоит в введении добавочного вектора
s
и рас-
ширенной функции стоимости
Q
(x
,
s)
, которая является квадратичной
по
x
при фиксированном
s
и минимум которой
min
s
Q
(x
,
s) =
J
(x)
для любого
x
. Если
Q
(x
,
s)
легко минимизируется по
s
(или если
существует точное решение), то расширенная функция
Q
(x
,
s)
мо-
жет быть оптимизирована с приемлемой эффективностью при помощи
итеративного координатного спуска.
Задача представления сигнала посредством переопределенного ба-
зиса отличается от более тривиальных обратных задач, таких как на-
хождение оригинала изображения. Основное внимание в последних
концентрируется на том, чтобы сделать обратную функцию непрерыв-
ной, что соответствует минимизации
`
2
-нормы
x
, которая не приводит
к некорректным решениям. Используется другой аспект регуляриза-
ции, определяющий однозначное решение среди большого множества
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3
13


