Рис. 6. Распределение напряжений
σ
33
в 1/8 ЯП упруго-пластического компози-
та в задаче Ж33, коэффициент армирования 0,35
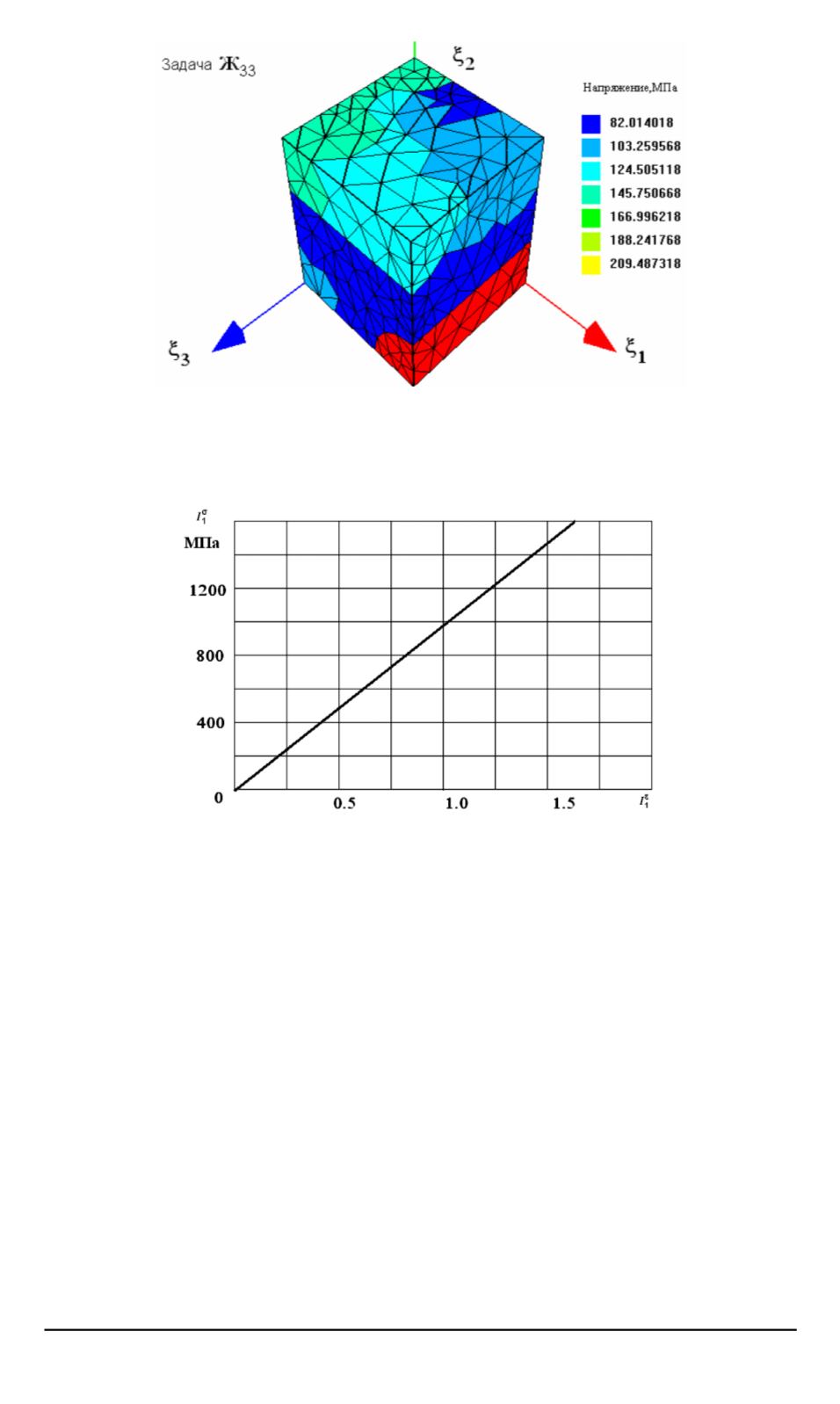
Рис. 7. Эффективная зависимость инварианта
I
σ
1
от
I
ε
1
(функция
I
σ
1
=
ϕ
1
(
I
ε
1
, I
ε
2
, I
ε
3
))
для упруго-пластического композита с коэффициен-
том армирования 0,35
от
I
ε
2
при различных фиксированных значениях инварианта
I
ε
3
(функ-
ция
I
σ
2
=
ϕ
2
(0
, I
ε
2
,
I
ε
3
)
приведены на рис. 8, а зависимости инвариан-
та
I
σ
3
от
I
ε
3
при различных фиксированных значениях инварианта
I
ε
2
(функция
I
σ
3
=
ϕ
3
(0
, I
ε
2
, I
ε
3
)
показаны на рис. 9. Этими вычисления-
ми проверялась возможность принятия простейшей модели (49) для
композита. Они показали, что такая модель может быть принята, так
как третий инвариант
I
ε
3
практически не влияет на зависимость меж-
ду вторыми инвариантами
I
σ
2
и
I
ε
2
, и наоборот, второй инвариант
I
ε
2
практически не оказывает влияния на эффективную зависимость меж-
ду третьими инвариантами. Этот вывод, по крайней мере, справедлив
для исследованного диапазона изменений характеристик матрицы, во-
локна и коэффициента армирования.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 1
43


