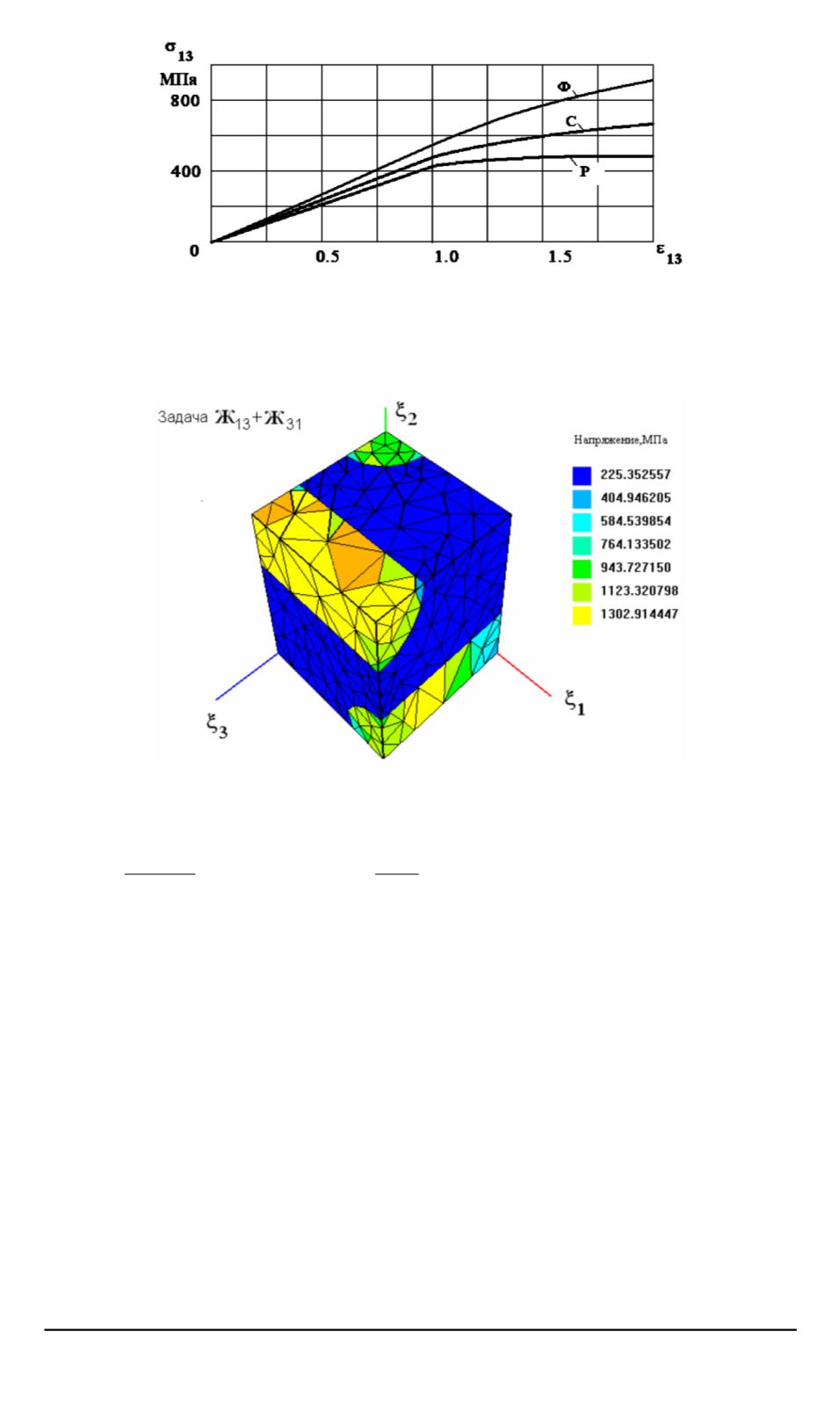
Рис. 4. Эффективные диаграммы:
напряжение
ˉ
σ
13
–деформация
ˉ
ε
13
для упруго-пластического композита (с), оценки
диаграммы по Фойгту (Ф) и Рейссу (Р)
Рис. 5. Распределение напряжений
σ
13
в 1/8 ЯП упруго-пластического компози-
та в задаче Ж13+Ж31, коэффициент армирования 0,35
ˉ
ε
13
=
1
−
ϕ
f
2
G
m
(1
−
ω
m
(ˉ
σ
13
)) +
ϕ
f
2
G
f
(1
−
ω
f
(ˉ
σ
13
)) ˉ
σ
13
(по Рейссу),
ˉ
σ
13
= 2(
G
m
(1
−
ϕ
f
)(1
−
ω
m
(ˉ
ε
13
))+
G
f
ϕ
f
(1
−
ω
f
(ˉ
ε
13
)))ˉ
ε
13
(по Фойгту),
где
G
m
,
ω
m
(ˉ
ε
13
)
,
G
f
,
ω
f
(ˉ
ε
13
)
— модули сдвига и функции пластич-
ности А.А. Ильюшина для матрицы и волокна. Проведенные расчеты
показали, что вычисления эффективных диаграмм деформирования
композита по этим приближенно-аналитическим методам приводят к
значительной погрешности (см. pис. 4); отличие от результатов, полу-
чаемых разработанным методом, достигает 50% по напряжениям.
На рис. 5 показано распределение напряжений
σ
13
в 1/8 ЯП упруго-
пластического композита в задаче Ж13+Ж31, а на рис. 6 — распреде-
ление напряжений
σ
33
в задаче Ж33.
Эффективная зависимость инварианта
I
σ
1
от
I
ε
1
(функция (49) вида
I
σ
1
=
ϕ
1
(
I
ε
1
,
0
,
0))
для упруго-пластического композита с коэффициен-
том армирования 0,35 показана на рис. 7. Зависимости инвариантов
I
σ
2
42
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 1


