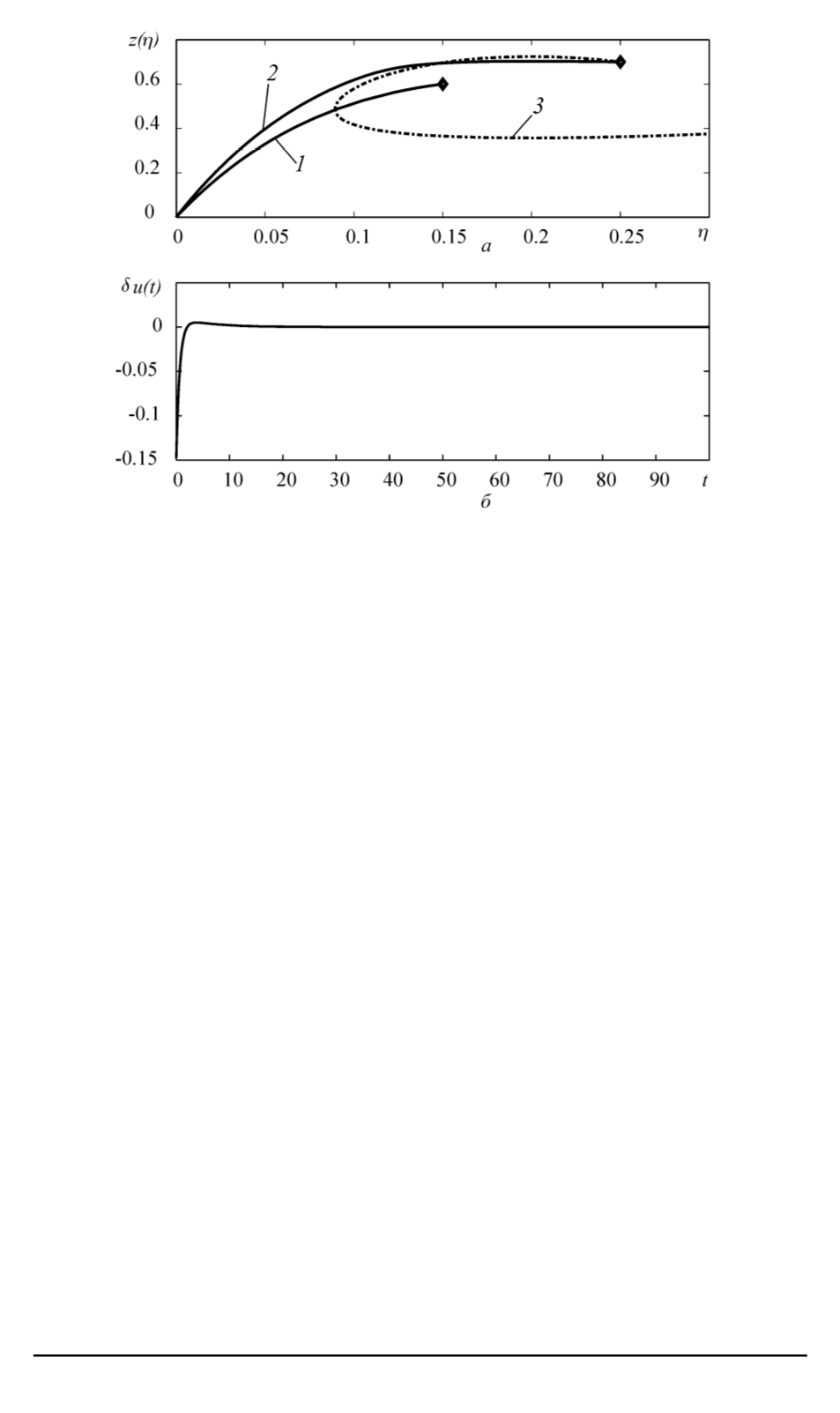
Рис. 3. Графики программной
1
, реализующейся стабилизированной
2
и неста-
билизированной
3
траекторий (
а
) и стабилизирующего управления (
б
)
Для численного моделирования примем
c
0
= 1
,
5
. На рис. 3 при-
ведены графики программной и реализующихся стабилизирован-
ной и нестабилизированной траекторий при
z
|
t
=0
=
z
(
t
) + 0
.
1
и
η
|
t
=0
=
η
(
t
) + 0
.
1
, а также график зависимости стабилизирующего
управления от времени.
Выводы.
Для аффинных динамических систем со скалярным упра-
влением и выходом, преобразуемых к нормальной форме, приведены
условия, при которых метод нелинейной стабилизации обеспечива-
ет равномерную асимптотическую или экспоненциальную стабилиза-
цию программного движения, соответствующего заданному измене-
нию выхода.
Стабилизация имеет место в переменных нормальной формы. Для
технических систем такие переменные часто имеют физическую ин-
терпретацию. В случае, если требуется стабилизация программного
движения в исходных переменных, проблема требует дополнительно-
го исследования.
Работа выполнена при финансовой поддержке гранта РФФИ
05-01-00840 и программы “Развитие научного потенциала высшей
школы
(
2006–2007
)
гг.)”, проект РНП 2.1.1.2381.
СПИСОК ЛИТЕРАТУРЫ
1. I s i d o r i A. Nonlinear control systems. 3rd ed. London, 1995.
2. S a s t r y S. Nonlinear systems: analysis, stability and control. Springer, 1999.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4
59


