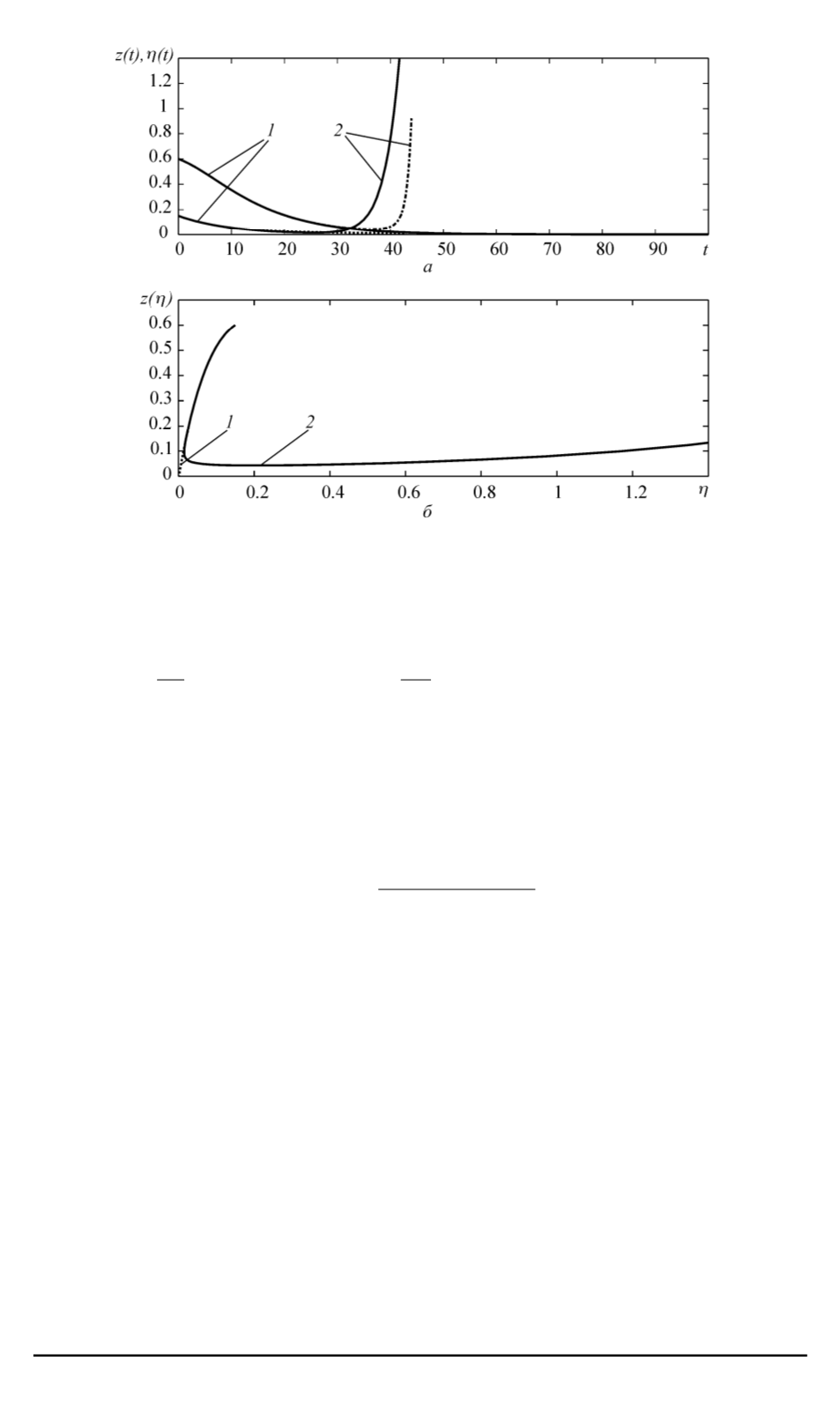
Рис. 2. Графики изменения переменных для программной
1
и реализующейся
2
траекторий в зависимости от
t
(
а
) и в виде
z
(
η
)
(
б
)
Элементы матрицы Якоби
∂
ˉ
q/∂
(
e, φ
)
имеют вид
∂
ˉ
q
∂e
=
a
2
(
φ
+
η
(
t
))
,
∂
ˉ
q
∂φ
=
−
k
2
+
a
2
(
z
(
t
) +
e
)
.
Из полученных соотношений видно, что матрица Якоби лишь локаль-
но ограничена в любой замкнутой окрестности точки
(
e, φ
) = (0
,
0)
.
Для стабилизации возьмем нестационарную обратную связь вида
(10), которая в данном случае имеет вид
δu
=
−
ˉ
f
(
e, φ, t
) +
c
0
e
ˉ
g
(
e, φ, t
)
,
(35)
где
ˉ
g
(
e, φ, t
) = 1
, а
c
0
>
0
— константа, определяющая свойства обрат-
ной связи.
Таким образом, для системы в отклонениях, соответствующей за-
данному программному движению системы (31) и замкнутой обратной
связью (35), выполняются условия
теоремы 2
. Следовательно, поло-
жение равновесия
(
e, φ
) = (0
,
0)
замкнутой системы локально экспо-
ненциально устойчиво.
Заметим, что все расчеты удобнее проводить в исходных пере-
менных
z
,
η
и обращение к переменым
e
,
φ
необходимо лишь для
теоретического анализа. В исходных переменных имеем
δu
=
−
(
k
1
z
−
a
1
zη
−
k
1
z
(
t
) +
a
1
z
(
t
)
η
(
t
) +
c
0
(
z
−
z
(
t
)))
.
В системе (31) при этом
u
=
u
(
t
) +
δu
.
58
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4


