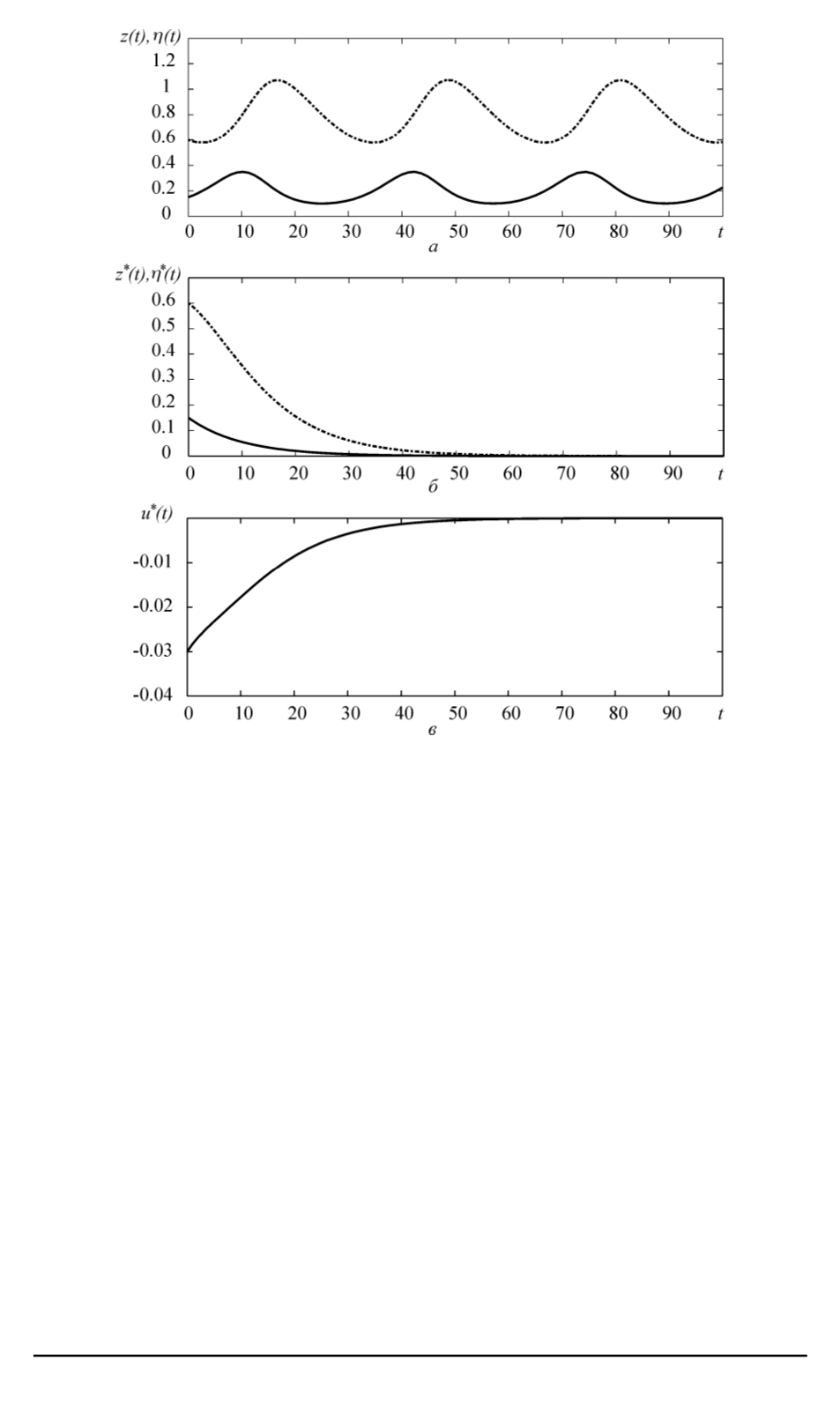
Рис. 1. Графики свободного движения системы (
а
), программной траектории (
б
)
и программного управления (
в
)
При приближении программной траектории к
z
= 0
в силу неустой-
чивости реализующаяся траектория по переменному
z
отклоняется от
программной. При существенном отклонении
z
(
t
)
от
z
(
t
)
неравен-
ство
p
(
z
(
t
))
>
0
может нарушиться, и положение равновесия
η
= 0
перестанет быть устойчивым. В рассматриваемом примере экспонен-
циальная устойчивость положения равновесия
η
= 0
уравнения (32)
гарантируется при
k
2
−
a
2
a
≥
c >
0
При выбранных значениях пара-
метров устойчивость нарушается при
z
(
t
)
≥
k
2
/a
2
= 0
,
8
.
Для стабилизации программной траектории воспользуемся тем,
что система (31) имеет вид соотношений (24), и при заданном измене-
нии выхода выполняются условия
теоремы 4
, т.е. нулевая динамика
системы в отклонениях экспоненциально устойчива в целом.
Заметим, что
ˉ
q
(
e, φ
) =
q
(
z
(
t
) +
e, η
(
t
) +
φ
)
−
q
(
z
(
t
)
, η
(
t
)) =
=
−
k
2
φ
+
a
2
(
z
(
t
) +
e
)
φ
+
a
2
eη
(
t
)
непрерывно дифференцируема в
R
2
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4
57


